Capacitor Charging and Discharging

This article explains capacitor charging, energy content and energy losses during the charge transfer

Capacitor Charging and Discharging

In electronic circuits, charging a capacitor from a voltage source is a common but critical event. Direct connection of an uncharged capacitor to a source can cause dangerously high inrush currents, potentially damaging semiconductors and the capacitor itself. To mitigate this, engineers employ pre-charge circuits with resistors and switches. This paper summarizes insights of capacitor charging dynamics, highlighting the role of resistance, inductance, and their impact on current peaks, oscillations, and energy dissipation.

Key Points

• Direct capacitor charging leads to very high inrush currents.
• Pre-charge resistors limit current and protect components.
• Series inductance reduces peak current but introduces oscillations.
• Total energy loss is governed by C∆V2/2, independent of inductance.
• In closed-loop inverters, added inductance may cause instability due to negative input resistance.

Basic Charge Storage and Discharge

When connected to a direct current (DC) voltage source, capacitors charge almost instantaneously, but they can discharge just as fast if shorted; however, with some resistance in place, the rate of charge and discharge is exponential rather than direct (Figure 1.).

Oscillators, waveform shapers and low-discharge power backup circuits are examples of electronics that leverage controlled charge and discharge rates.

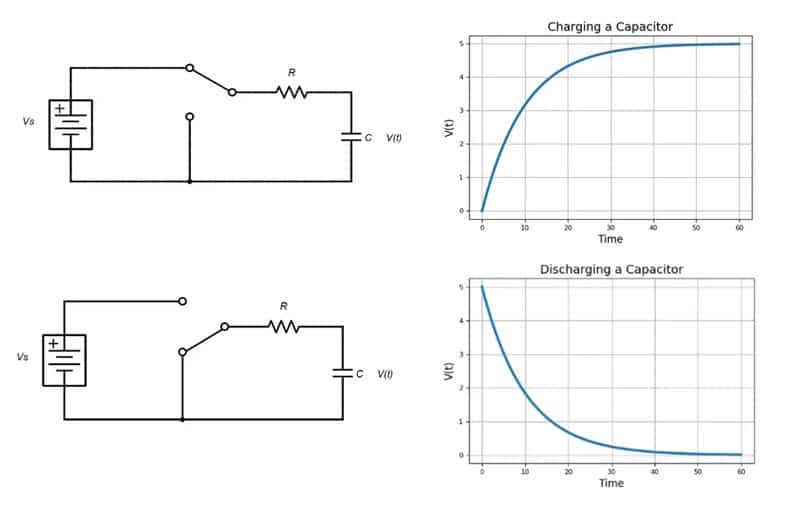
Capacitor Charging Basics

When a capacitor of capacitance C is charged from a voltage source V, the stored energy is:

E = 1 2 C V2

This energy must be supplied by the source, and in a resistive circuit, it is dissipated as heat. Without inductance, the peak current is approximately:

Ipeak = ∆V R

Role of Inductance

Introducing series inductance L changes the dynamics. The circuit becomes an RLC network, and the current follows a damped oscillatory response. The natural resonant frequency is:

ω = 1 LC

As inductance increases, the peak current decreases, but oscillations appear and the charging time extends. Despite these changes, the total energy dissipated in the resistor remains nearly constant.

Impact of Resistance

Sweeping resistance values in simulation revealed that lower resistance increases peak current and oscillations, while higher resistance damps oscillations and reduces peak current. The LC resonance frequency remains unchanged, but the damping factor varies with resistance.

Impact of Insulation Resistance IR and Leakage Current

The circuit diagram and charging curve for a capacitor are shown in Figure 2.

The charging current to the capacitor is shown in Figure 3. (circuit diagram as in Figure 2.). If the capacitor is ideal the current would rapidly attain the limiting value corresponding to the IR. The ideal current curve is designated I_C-ideal. But because the polarization in the dielectric requires a finite time for dipoles to reorient the real charging current follows the curve I_{C-polarization}.

Closed-Loop System Considerations

While inductance is beneficial in reducing inrush current, in closed-loop inverter systems it can introduce instability. This occurs because the input of a regulated converter can exhibit negative resistance: as input voltage rises, input current decreases to maintain constant power. Coupled with an LC resonance, this negative resistance may lead to oscillations and instability.

Fundamental Loss Analysis

Simulation and theoretical analysis show that regardless of resistance or inductance, the energy dissipated during charging converges to the same value: half of the supplied energy. This is explained by charge conservation:

the source delivers

E_source = Q · V_in

while the capacitor stores only half of that energy, with the remainder dissipated as heat.

The Diode–Inductor Case

Introducing an inductor and diode changes the dynamics. The inductor stores energy losslessly, and the diode enforces unidirectional current. In this case, the capacitor voltage can rise above the source voltage, approaching twice V_in for very low resistance. As a result, the capacitor stores more energy, and the fraction lost in resistive elements decreases. This explains why measured losses are lower in high‑Q inductor–diode circuits.

Educational Implications

The analysis highlights a key paradox: while direct charging always wastes half the energy, clever circuit arrangements can reduce losses. This principle underpins boost converters, resonant switched‑capacitor converters, and energy recovery techniques. Understanding these fundamentals is essential for efficient power electronics design.

Conclusion

Capacitor charging dynamics are governed by the interplay of resistance, inductance, and capacitance. For practical design, pre-charge circuits with resistors are essential, and inductance must be carefully considered—beneficial for limiting current, but potentially destabilizing in closed-loop systems. Understanding these trade-offs is crucial for robust power electronics design.

Capacitor charging losses are an unavoidable reality in direct RC/RLC circuits, with half of the supplied energy always dissipated. However, by introducing inductors and diodes, designers can alter the voltage dynamics and reduce losses significantly. This knowledge is not only academically interesting but also practically relevant to modern converter design, energy harvesting, and efficient power management systems.