This blog article from Knowles Precision Devices perform a deep dive on what bandwidth is and why we need to consider bandwidth when selecting a filter.
In previous article, we provided a brief overview of five key filter specifications to understand, one of which was bandwidth. In this post, we will dive deeper into bandwidth by looking at the history of bandwidth, how bandwidth dictates data rate, and why the type of filter required will vary depending on an application’s bandwidth requirements.
First, let’s look at why bandwidth is important. In general, bandwidth is defined as the width of the passband of the bandpass filter and expressed as the frequency difference between the lower and upper 3 dB points. Bandwidth will dictate the data rate, or how quickly we can send information through a channel such as an optical fiber or a section of the radio spectrum.
A Historical Review of How to Calculate Bandwidth
To better understand bandwidth, let’s look back at some of the historical work that laid the foundation for how to consider this specification. In the 1920s, when Harry Nyquist was working on the telegraph at AT&T’s Department of Development and Research, the notion of the Nyquist Rate emerged from his work. In short, this is the theoretical minimum system bandwidth needed to detect Rs symbols per second is Rs/2 hertz.
A way to look at this more simply is to think about how signals behave in time when they are band limited. A signal such as a series of pulses that is band limited in the frequency domain gets distorted and smeared out in time. To stop these smeared-out pulses from overlapping and becoming indistinguishable at a detector, there needs to be enough bandwidth to contain all, or at least the majority, of the frequency components that make up that signal pulse. It turns out, the amount of bandwidth we need gives us the Nyquist Rate, which says that for things to make sense at the other end of a transmission, we can send pulses as fast as twice the channel bandwidth, but no faster.
Similarly, to understand why bandwidth follows when we need to increase data rate, let’s look at the Shannon-Hartley theorem that was developed in 1948 by Claude Shannon and Ralph Hartley, both researchers at Bell Labs. This theorem tells us that the maximum amount of error-free digital data that can be transmitted over a channel of a given bandwidth in the presence of noise, which is calculated using the following equation:
where:
- C = Channel capacity in bits/second
- M = Number of channels (e.g. the MIMO order)
- B = Bandwidth in hertz
- S = transmit power, in watts
- N = noise on channel, in watts
- S/N = signal to noise ratio
To increase channel capacity (data rates) we can increase bandwidth, the number of channels, or transmit power (S) or decrease the noise on the channel (N). Since this post is focused on bandwidth, we won’t get into too much detail about this, but it is worth noting that you can reduce N and increase channel capacity with filtering. For example, by including a filter with very low insertion loss, you could improve the overall noise figure, or you could address any aliasing effects that would bring out of band noise in the band of interest using a really good filter.
How Does an Application’s Bandwidth Requirements Impact Filter Selection?
Bandwidth requirements vary widely by application as shown in Figure 1.
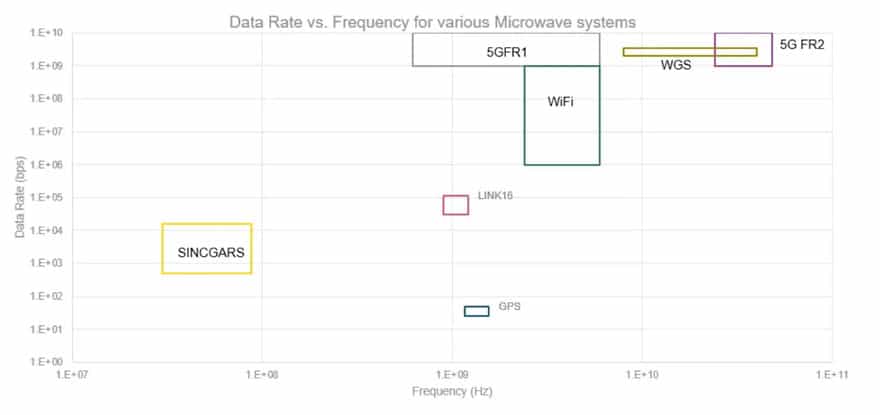
Since different applications require different data rates to successfully transmit signals without introducing noise, different types of filters are necessary as bandwidth and frequency increase. In short, the type of filter you need depends on where you are on the frequency versus bandwidth plot. More specifically, if you look back to Five Key Filter Specifications again, we also noted that we can look at the relative, or fractional, bandwidth of the filter. This is the ratio of a filter’s bandwidth to its center frequency. As shown in Figure 2, different filter technologies are capable of different fractional bandwidths.
Throughout this post, we looked at several different aspects of bandwidth, including how bandwidth is driven by the required channel capacity, or data rate; how different systems have different data rates, and hence, different bandwidths; and how different filter technologies are used to meet these varying bandwidth needs. In the next post in this series, we will spend more time exploring poles and zeros and how these are tools a filter designer can manipulate to improve a filter’s response.