This article by Dr. V. Azbel, an Independent consultant on tantalum capacitors, introduces software-based approach on assessing the risk of tantalum capacitor anode overheating by modeling and practical solutions example.
Introduction
The development of a tantalum capacitor (TC) anode requires precise control over sintering and forming processes. One of the key challenges is anode overheating during the formation stage, which is associated with the growth of the amorphous tantalum pentoxide (Ta₂O₅) layer and its impact on the thermal conductivity of the anode neck. Traditional methods for calculating anode parameters require significant time and do not allow for an accurate assessment of overheating risks.
This study proposes a software-based approach to optimizing anode parameters. The developed model quantitatively evaluates the influence of structural characteristics and technological parameters on the anode’s thermal balance. The primary assessment criterion is the Q/Wa coefficient, where Q represents heat dissipation and Wa denotes the energy released. To minimize the risk of overheating, the Q/Wa value must exceed 10.
Modeling Methodology
The modeling of anode thermal balance is based on a geometric representation of its structure. The key stages of the methodology include:
- Modeling the Porous Structure of the Anode
- The anode represents a set of spherical particles forming pores and necks (see Fig. 1a, b).
- The geometry of the neck critically affects thermal conductivity and electric current distribution.
- Oxide Layer Formation Process
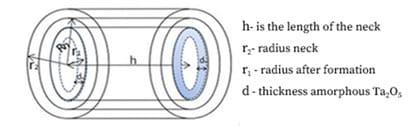
- During the formation stage, the amorphous Ta₂O₅ Sooner grows inward and outward from the neck surface (see Fig. 2a, b).
- The growth of the oxide layer (d) reduces the cross-sectional area of the neck (S = π⋅(Rn)²/4) (see Fig. 3), increasing resistance and the released energy Wa.
- If the oxide layer reaches a critical thickness, the neck becomes completely blocked, leading to anode failure.
- Evaluation of Heat Transfer in the Neck Region
- The primary mechanisms (see Appendix) include the thermal conductivity of tantalum and the amorphous Ta₂O₅ layer.
- When the oxide’s thermal conductivity is low, heat accumulates, increasing the likelihood of local overheating.
- Determining the Q/Wa Coefficient
- This coefficient is calculated based on the thermal conductivity, resistance, and neck geometry.
- Experimental data* confirm that for stable anode operation, Q/Wa > 10.
- *Tested using tantalum capacitor anodes that have passed reliability testing.
Influence of Anode Parameters on Overheating Risk
Factors affecting heat distribution and the likelihood of overheating include:
- Neck size and anode porosity: A smaller neck cross-sectional area increases the surface area (see Fig. 4). However, this also increases electrical resistance and the risk of localized heating.
- Anode Thickness and Shape: Complex geometry complicates heat dissipation, creating localized overheating zones.
- Transition Layer Between Ta and Ta₂O₅: Reduces thermal conductivity and increases resistance.
Advantages of the Software-Based Approach
The developed software allows for:
- Automatic optimization of anode parameters.
- Prediction of overheating risk based on Q/Wa.
- Reduction in the number of experiments and time required for developing new TC designs.
- Elimination of subjective errors in design.
Conclusions
Modeling the anode’s thermal balance, considering neck structure and the oxide layer formation mechanism significantly improves the accuracy of overheating risk predictions. The developed software (with a calculation algorithm flowchart presented in Table 1, see Appendix) provides a convenient tool for the automated selection of optimal anode parameters, enhancing reliability and reducing failure probability. Future model improvements may include accounting for the mechanical properties of the anode for a more detailed analysis.
Integration of the Software into the Anode Production Process
The developed software is designed to calculate the hypothetical risk of overheating, serving as a key tool for optimizing anode parameters. Based on this foundation, an advanced version has been created, enabling real-time detection of issues within the ongoing production process.
The new software version incorporates real-time integration of experimental data, further increasing the accuracy of overheating risk predictions. This functionality allows for continuous monitoring and adaptive adjustments, ensuring stable process parameters and minimizing failure risks.
Appendix
The table below clearly illustrates the dependence of BET, capacitance, and forming voltage on the size of primary powder particles.
BET determines the range of powder applications—from high-voltage to low-voltage capacitors.
The primary influencing factor is the size of the primary particles while modifying the pressing density and sintering temperature further adjusts the properties.
Sintering regulates porosity (capacitance) and the neck size between grains (forming voltage), allowing the material to be tailored to the required parameters.
This information was used to develop the program flowchart below, which enables the selection of optimal powder parameters based on specified capacitance and operating voltage requirements.
Experimental data (CABOT, H.C. Starck) used in program development. Size prime particles powder- CABOT
Examples of the program’s operation
Table 2 presents data on the influence of the anode mass within a single design on the risk ofoverheating.
Table 3 shows the influence of different electrolysis parameters applied to a single-sintered pellet design on the risk of anode overheating.
Heat Transfer and Energy Dissipation Mechanisms in the Neck Region, used in Software
The main mechanisms include:
- Heat Transfer Through the Cross-Sectional Area of the Neck (q):
q = k⋅S⋅ΔT/h, where k is the thermal conductivity of tantalum (0.4 W·m⁻¹·K⁻¹), ΔT is the temperature difference, which can reach 450°C at the onset of amorphous film crystallization.
- Heat Transfer Through the Surface of the Amorphous Film (Q):
Q = k1⋅A⋅ΔT/d, where k₁ is the thermal conductivity of the amorphous film (0.7 W·m⁻¹·K⁻¹), A is the surface area of the film, and d is its thickness.
- Energy Dissipation in the Neck
The reduction of the neck’s cross-sectional area due to increasing forming voltage raises electrical resistance, leading to an increase in dissipated energy (Wa). According to the proposed model, this energy is calculated as:
Wa = Ir²⋅ρ⋅h/S, where Ir is the forming current, ρ is the resistivity, h is the neck length, and S is the cross-sectional area:
S = π⋅L²/4, where L=Rn (see Fig. 3).
- Risk of Complete Neck Blockage
If the forming voltage exceeds the optimal level, the radius of the oxide layer (r₁) becomes equal to the radius of the tantalum core (Rn). This results in complete neck blockage, a reduction in capacitance, and an increased risk of failure.