Current Sense Transformer and its Calculation

By Tomáš Zedníček
3 hours Ago

This paper edited from original YAGEO Group technical article provides brief comparison of current sense technologies and introduces main markets and applications where current sense transformer (CST) technique is applicable. CST selection guidance with a real application case study is proposed.

Key Takeaways

This article discusses current sense transformer (CST) technology, highlighting its accuracy, isolation, and efficiency in energy measurement.
CSTs are ideal for high-frequency applications, outperforming shunt resistors and Rogowski coils in specific scenarios.
The selection of CSTs involves assessing parameters like RMS current rating, volt-second product, and mechanical constraints.
A case study illustrates the application of CSTs in automotive battery management systems, demonstrating their low measurement error.
YAGEO Group provides a range of CST solutions that meet rigorous safety standards across various industries.

Introduction

As energy efficiency becomes a defining requirement for modern electronic systems, the ability to measure current with high precision has never been more critical. Accurate current monitoring enables engineers to optimize power conversion, detect faults, and guarantee compliance with stringent safety standards.

Different application domains call for different sensing strategies. Broadly, current sensing can be divided into three categories:

DC: DC current measurement (e.g., battery monitoring in EVs or energy storage systems)
LF: Low-frequency measurement (50/60 Hz power distribution networks)
HF: High-frequency measurement (switch-mode power supplies operating above 40 kHz)

Current-frequency domain

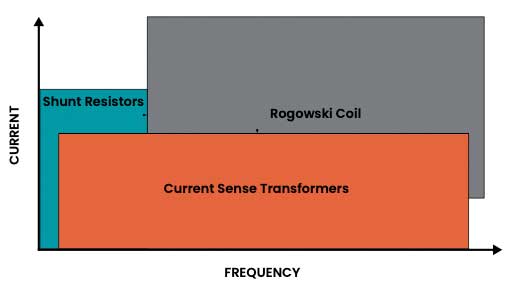
While several sensing technologies are available—including shunt resistors, Rogowski coils, and current sense transformers (CSTs)—the CST stands out when accuracy, galvanic isolation, and efficiency at high frequencies are essential.

Technology landscape: Comparing sensing methods

Selecting the right current sensing technology requires balancing trade-offs in accuracy, cost, power dissipation, isolation, and frequency response.

Technology	Advantages	Limitations	Typical applications
Shunt resistor	Low cost, simple, no phase error	High loss, no isolation	Low-power DC/DC, battery monitoring
Hall-effect sensor	High accuracy, galvanic isolation, DC & AC sensing	Expensive, requires power, temperature sensitive	Industrial drives, medical, precision systems
Current sense transformer (CST)	Accurate, low-loss, isolated, good EMI immunity	No DC response, core saturation at very low frequency	SMPS, AC line monitoring, solar/UPS
Rogowski coil	Wide bandwidth, no core saturation, high current	Needs integrator, poor low-frequency response	Transient analysis, arc fault detection, power quality

The decision often comes down to whether the application requires high efficiency and strong isolation at high frequency—an area where CSTs consistently outperform alternatives.

Application domains

CSTs have become indispensable in areas where system efficiency and safety are paramount. Their combination of low power dissipation, strong isolation, and EMI robustness make them well-suited for:

SMPS: Precise current feedback for regulation and protection.
High-voltage monitoring: Safe measurement of current in systems requiring reinforced isolation.
Solar inverters and UPS: Supporting reliable conversion and uninterrupted operation.
Industrial automation: Providing accurate sensing in electrically noisy environments.

Operating principles

The operation of a current sense transformer is grounded in the fundamentals of electromagnetic induction. When an AC current flows through the primary winding, it induces a proportional current in the secondary. This secondary current, when passed through a terminating resistor, produces a measurable voltage directly proportional to the original current.

Ideal relationships

(1) Sense current vs. primary current (ideal CST)

IPrim=N⋅IsenseI_{\text{Prim}} = N \cdot{I_{\text{sense}} }

Where N means a turn-ratio. Voltage sense is a direct measurement of a primary current I_prim

(2) Sense voltage across terminating resistor

Vsense=RT⋅IprimNV_{\text{sense}} = R_T \cdot \frac{I_{\text{prim}}}{N}

Non-ideal behavior and losses

Flowing primary current slightly differs from measured current value, as the core of current sense transformers needs to be magnetized by magnetizing current. Hysteresis losses (I_Fe) are typically negligible for CSTs. The magnetizing current can be identified from basic parameters as a source of amplitude error.

(3) Primary current composition

Iprim=Imeas−ImagI_{\text{prim}} = I_{\text{meas}} – I_{\text{mag}}

*Fig. 2a) Simplified Operating Principle of CST; Fig 2b) right: Example photographs of CST products*

Magnetic modeling and optimization

Imag=(VSenseN)⋅dutycycleLm[mH]⋅Freq[kHz]I_{\text{mag}} = \frac{\left( \frac{V_{\text{Sense}}}{N} \right) \cdot \text{duty}_{\text{cycle}}}{L_m\,[\text{mH}] \cdot \text{Freq}\,[\text{kHz}]}

To optimize CST parameters, magnetic Finite Element Method (FEM) analysis is used. Magnetic field distribution analysis helps determine magnetic losses and phenomena related to phase shift between measured and sensed current values.

VSense=RT⋅IPrimN=RT⋅Imeasured−ImagNV_{\text{Sense}} = R_T \cdot \frac{I_{\text{Prim}}}{N} = R_T \cdot \frac{I_{\text{measured}} – I_{\text{mag}}}{N}

*Fig. 3) Example magnetic field distribution within CST (shape core version), B [Gauss]*

Comparator-based measurement

A CST integrates easily into analog or digital measurement systems. The sense voltage—i.e., the voltage drop across the external terminating resistor R_T – is commonly used as the comparator input voltage.

(4) Comparator input and output behavior

Comparator’s tasks is to compare measured V_sensevalue to assigned reference voltage V_ref, where V_ref value typically defines maximum voltage drop we can measure on R_T – under I_sense is flowing:

Vref=max⁡(Vsense)=RT⋅IsenseV_{\text{ref}} = \max(V_{\text{sense}}) = R_T \cdot I_{\text{sense}}

As result – we get final referenced output voltage V_out, which can be directly used for discrete or analog regulation systems or for monitoring purpose.

*Fig. 4) Functional electric schematic of CST in measurement circuit with burden resistor R_T*

Current sense transformer selection guidelines

Successful implementation of CSTs requires careful attention to design parameters:

RMS current rating: Prevents overheating under maximum load.
Volt-second product / flux density: Ensures the magnetic core avoids saturation.
Terminating resistor (R_T): Balances output voltage levels against measurement accuracy.
Isolation voltage: Must meet safety regulations such as basic, functional, or reinforced insulation.
Mechanical constraints: Package dimensions, creepage, and clearance distances must fit within system requirements.

Step 1. Product series choice based on safety

Define current, insulation, and size constraints. Manufacturer datasheets provide specifications for mechanical dimensions, insulation ratings, clearance distances, and safety certifications. YAGEO catalog CST products are suitable for applications up to 1.5 kV and meet creepage, clearance, and reinforced insulation requirements.

*Fig. 5) YAGEO Catalog Product Portfolio range of CST*

The catalog portfolio covers mechanically optimized constructions for applications up to 50 A with a wide range of turns ratios. Some products support measurement frequencies up to 2 MHz. Full custom designs are available for wider current ranges.

Step 2. Part number choice guidance

Define the application, the comparator and its available reference voltage V_ref, and the operating frequency or frequency range. Use a first-pass simplified analysis to select the required turns ratio and V_ref.

Input parameters: Measured peak primary current (I_pk), duty cycle (D), maximum desired sense voltage (V_sense,max) based on comparator V_ref.

Working point and flux density

Selection starts with CST turns ratio based on working point (flux density B) under given conditions: frequency (f), duty cycle (D), and V_ref. Datasheets specify the effective core area A_e used in flux estimations.

(5) Flux density working point (conceptual)

B[Gauss]=1Ae⋅Vref⋅DutycycleN⋅FreqkHzB\, [\text{Gauss}] = \frac{1}{A_e} \cdot \frac{V_{\text{ref}} \cdot \text{Duty}_{\text{cycle}}}{N \cdot \text{Freq}_{\text{kHz}}}

To stay in the linear part of the core B/H characteristic, the working point B should typically be within 250–2200 Gauss, with the absolute maximum specified in the datasheet. This region determines a feasible solution domain for part selection.

*Fig. 6) Example of Flux Density vs. Frequency characteristics for CST calculated for constant V_ref condition*

Higher frequencies generally require lower turns counts and higher V_ref, while lower frequencies require higher turns ratios and may use lower V_ref. The turns ratio N impacts sensitivity: higher N lowers the working point and V_sense, reducing sensitivity.

Terminating resistor calculation

Once a part number is selected, determine the terminating resistor value.

(6) Terminating resistor from peak conditions

RT=VSense⋅NIprimR_T = \frac{V_{\text{Sense}} \cdot N}{I_{\text{prim}}}

Step 3. Measurement error, signal delay & sensitivity

Analyze amplitude and phase shift error. Amplitude error is mostly caused by CST losses, where magnetizing current plays a significant role and is typically small and linear (often < 2%). Phase error depends on burden and parasitics and should be minimized during design.

(7) Amplitude error due to magnetizing current

IError[%]=(1−|Imeasured−ImagImeasured|)⋅100%I_{\text{Error}}[\%] = \left(1 – \left| \frac{I_{\text{measured}} – I_{\text{mag}}}{I_{\text{measured}}} \right| \right) \cdot 100\%

(8a) Phase shift (general)

a[Deg]=atan⁡(RT+RDCsec2⋅π⋅FreqkHz⋅L[mH])a[\text{Deg}] = \operatorname{atan} \left( \frac{R_T + R_{\text{DCsec}}}{2 \cdot \pi \cdot \text{Freq}_{\text{kHz}} \cdot L[\text{mH}]} \right)

(8b) Phase shift (simplified when R_T ≫ R_DC,sec)

a[Deg]=atan⁡(RT2⋅π⋅FreqkHz⋅L[mH])a[\text{Deg}] = \operatorname{atan} \left( \frac{R_T}{2 \cdot \pi \cdot \text{Freq}_{\text{kHz}} \cdot L[\text{mH}]} \right)

(8c) Maximum phase error estimate

Errora[%]=(1−cos⁡a)⋅100%(8c)\text{Error}_a[\%] = (1 – \cos a) \cdot 100\% \tag{8c}

Sensitivity

(9a) Sensitivity (V/A)

sensitivity[V/A]=(Vsense[V]Imeasured[A])\text{sensitivity}\,[\text{V/A}] = \left( \frac{V_{\text{sense}}\,[\text{V}]}{I_{\text{measured}}\,[\text{A}]} \right)

(9b) Sensitivity error

IError[%]=(1−|Imeasured−IimagImeasured|)⋅100%I_{\text{Error}}\,[\%] = \left(1 – \left| \frac{I_{\text{measured}} – I_{\text{imag}}}{I_{\text{measured}}} \right| \right) \cdot 100\%

Case study: High-accuracy CST performance

Consider an automotive application (e.g., BMS) with V_ref = 15 V, estimated peak current I_pk = 29 A, frequency f = 200 kHz, and duty cycle D = 0.8. Mechanical constraints: maximum 13 mm × 11 mm × 8 mm.

Step 1: Series choice

Automotive applications require functional insulation. With the noted mechanical constraints, select CSFA series and use the YAGEO Group product selector to locate a suitable range.

*Fig. 8) Screenshot of YAGEO Group Product Selection Tool*

Step 2: Part selection and working point

Open the datasheet to review parameters. In this case, four turns ratios are available for the PMS9494 product range.

*Fig. 9) Example of datasheet (Series CSFA – product range PMS9494)*

To better understand, we calculate working point based (flux density B) according to Eq.5 based on our automotive application conditions: Freq. = 200kHz, Vref=15V, DutyCycle=0.8. This equation is also specified in datasheet (Fig. 9, Notes, Pkt 4). Calculations can be systemized as in Table 2:

N	DutyCycle	Vref [V]	Freq [kHz]	Ipk [A]	B [Gauss]	R_sense [Ω]
50	0.8	15	200	29	2256	25.86207
100	0.8	15	200	29	1128	57.72414
150	0.8	15	200	29	752	77.58621
200	0.8	15	200	29	564	103.483

The N=50 option exceeds the suggested limit of B = 2200 Gauss and is excluded. The 1:100 option (PMS9494.100NLT) places B mid-range within the recommended window, providing flexibility for wider switching frequency or overcurrent.

RT=Vref⋅NIpkR_T = \frac{V_{\text{ref}} \cdot N}{I_{\text{pk}}}

RT=(15V⋅100)29A=51,72[Ω] R_T = \frac{(15\,\text{V} \cdot 100)}{29\,\text{A}} = 51{,}72\, [\Omega]

From Eq. (6), the terminating resistor for the selected part is approximately R_T ≈ 50 Ω. The secondary winding DCR is < 10% of R_T and has negligible influence on phase shift under these conditions.

Error and sensitivity estimates

Previous calculated values of B and RT allows us to calculate the amplitude error of the magnetizing current:

Imag=(VsenseN⋅dutycycle)Lm[mH]⋅FreqkHz I_{\text{mag}} = \frac{\left( \frac{V_{\text{sense}}}{N} \cdot \text{duty}_{\text{cycle}} \right)}{L_m\,[\text{mH}] \cdot \text{Freq}_{\text{kHz}}}

Imag=((14.5100)⋅0.8)÷(2.2⋅200)=0.28mAI_{\text{mag}} = \left( \left( \frac{14.5}{100} \right) \cdot 0.8 \right) \div (2.2 \cdot 200) = 0.28\,\text{mA}

Amplitude error due to magnetizing current is very small. Example calculation yields approximately 0.00154%, indicating the magnetizing current component is not measured.

IError[%]=(1−|Imeasured−ImagImeasured|)⋅100%I_{\text{Error}}[\%] = \left(1 – \left| \frac{I_{\text{measured}} – I_{\text{mag}}}{I_{\text{measured}}} \right| \right) \cdot 100\%

IError[%]=(1−|29−0.002829|)I_{\text{Error}}[\%] = \left(1 – \left| \frac{29 – 0.0028}{29} \right| \right)

100%=0,00154%100\% = 0{,}00154\%

Simplified phase shift calculation indicates a very low signal shift

a[Deg]=tan−1⁡(RT2⋅π⋅FreqkHz⋅L[mH])a\,[\text{Deg}] = \tan^{-1}\left( \frac{R_T}{2 \cdot \pi \cdot \text{Freq}_{\text{kHz}} \cdot L\,[\text{mH}]} \right)

a[Deg]=tan−1⁡(50[Ω]2⋅π⋅200[kHz]⋅2.2[mH])=tan−1⁡(502763)=tan−1⁡(0.018)=1.037∘a\,[\text{Deg}] = \tan^{-1}\left( \frac{50\,[\Omega]}{2 \cdot \pi \cdot 200\,[\text{kHz}] \cdot 2.2\,[\text{mH}]} \right) = \tan^{-1}\left( \frac{50}{2763} \right) = \tan^{-1}(0.018) = 1.037^\circ

Errorα[%]=(1−cos⁡α)⋅100%=(1−0.99984)⋅100%=0.0164% \text{Error}_{\alpha}\,[\%] = (1 – \cos{\alpha}) \cdot 100\% = (1 – 0.99984) \cdot 100\% = 0.0164\%

In this configuration, the measurement error is only 0.0164% and demonstrates exceptional accuracy achievable with well-designed CSTs.

Sensitivity of selected part number under application requirements will be:

sensitivity[V/A]=Vsens[V]Iprim[A]=Isens[A]⋅Rf[Ω]Iprim[A]=14.5[V]29[A]=0.5[V/A]\text{sensitivity}\,[\text{V/A}] = \frac{V_{\text{sens}}\,[\text{V}]}{I_{\text{prim}}\,[\text{A}]} = \frac{I_{\text{sens}}\,[\text{A}] \cdot R_f\,[\Omega]}{I_{\text{prim}}\,[\text{A}]} = \frac{14.5\,[\text{V}]}{29\,[\text{A}]} = 0.5\,[\text{V/A}]

Errorsensitivity[%]=Vsens−VrefVref⋅100%=(14.5−15)15⋅100%=0.033⋅100%=3.3%\text{Error}_{\text{sensitivity}}\,[\%] = \frac{V_{\text{sens}} – V_{\text{ref}}}{V_{\text{ref}}} \cdot 100\% = \frac{(14.5 – 15)}{15} \cdot 100\% = 0.033 \cdot 100\% = 3.3\%

Choice of terminating resistance influence sensitivity and sensitivity error.

Conclusion

YAGEO Group offers a wide range of current sensing solutions covering the full frequency range, including current sense transformer solutions applicable across diverse market segments.

Current sense transformers uniquely combine accuracy, galvanic isolation, and low-loss operation, making them the technology of choice for high-frequency AC current measurement. With careful selection and design, CSTs help meet stringent safety standards while delivering long-term reliability and efficiency in demanding applications such as SMPS, solar inverters, and industrial automation systems. While measurement errors are very low, proper adjustment to the measurement system is required for best results.

As energy efficiency accelerates, CSTs will continue enabling next-generation power systems. CSTs exhibit low measurement error compared to shunts and Rogowski coils due to minimal temperature rise, shielding against external EM fields, and lower energy dissipation than shunts.

Download the article in pdf from YAGEO Group website

FAQ about Current Sense Transformers

What is a Current Sense Transformer (CST)?

A Current Sense Transformer is a device used to measure AC currents with high accuracy, galvanic isolation, and low power loss. It is especially effective in high-frequency applications such as switch-mode power supplies, solar inverters, and industrial automation.

How does a CST compare to other sensing methods?

Compared to shunt resistors, Hall-effect sensors, and Rogowski coils, CSTs offer superior efficiency and isolation at high frequencies. They are unsuitable for DC measurement but excel in AC and high-frequency domains.

What are the main application domains of CSTs?

CSTs are widely used in SMPS for regulation and protection, high-voltage monitoring, solar inverters and UPS systems, and industrial automation where EMI robustness is critical.

What factors influence CST accuracy?

Accuracy is influenced by magnetizing current, core permeability, hysteresis, and parasitic capacitances. Proper design and FEM analysis help minimize amplitude and phase errors.

How do engineers select the right CST?

Selection depends on RMS current rating, flux density limits, terminating resistor value, isolation voltage, and mechanical constraints. Datasheets and product selectors guide the choice of part number.

How to Select a Current Sense Transformer

Step 1: Define application requirements
Identify current range, insulation needs, and mechanical size constraints. Check datasheets for compliance with safety standards such as creepage, clearance, and reinforced insulation.
Step 2: Choose product series and part number
Use manufacturer product selectors to find suitable CST series. Select a part number based on comparator reference voltage, operating frequency, and turns ratio.
Step 3: Calculate terminating resistor
Determine the resistor value using peak current and desired sense voltage. Ensure the resistor balances signal quality and measurement accuracy.
Step 4: Analyze measurement errors
Evaluate amplitude and phase errors. Magnetizing current typically causes small amplitude errors, while phase errors must be minimized for precise power monitoring.
Step 5: Validate with case study
Perform calculations under real application conditions (e.g., automotive BMS). Verify flux density, resistor values, and sensitivity to ensure compliance with design targets.

Categories: e-PassiveBlog, Inductors, Inductors e-Blog, Transformers
Tags: ABC of Inductors Yageo