The article defines the other basic principles of magnetism, magnetic and inductor components – Magnetic Induction, Magnetic Flux and Faraday’s Law.
Magnetic induction B
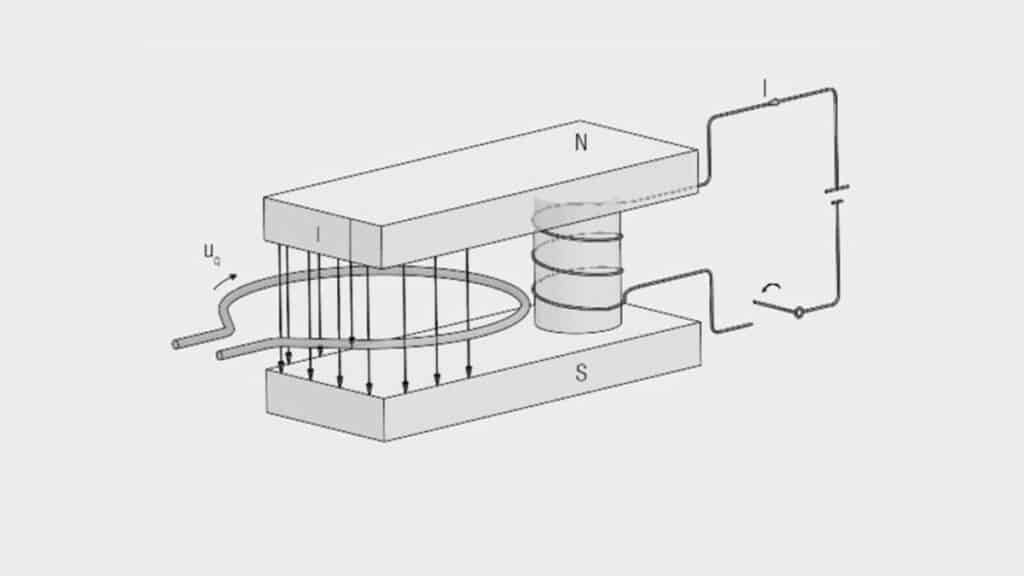
A potential is induced in a conductor loop if the magnetic field passing through the conductor loop changes with time.
The surge in potential over the area of the loop is known as the magnetic induction B. Like the magnetic field strength, the magnetic induction B is a vector quantity.
The following relationship applies for the magnetic induction B:
The magnetic induction (B) is the quotient of the induced potential surge:
and the product of the winding turns (N) and the windings area (A) of the induction coil.
The unit of magnetic induction (B) is the Tesla (T) = Vs/m2.
The magnetic induction B and the field strength H are proportional to one another. The constant of proportionality is the magnetic field constant (μ0), given by experimental measurement.
In vacuum and also with sufficient accuracy for air, this leads to:
The magnetic induction (BL) in air for the above example is then given by:
Magnetic Flux F
The magnetic flux (F) is the scalar product of the magnetic flux density (B) and the area vector (dA).
If (B) passes perpendicular through the area and the field is homogeneous:
The unit of magnetic flux (F) is the same as that of the voltage surge (Vs) (Voltsecond) or Weber (Wb).
Faraday’s law
Up until now we have considered static magnetic fields. If the magnetic flux changes with time, a voltage U is induced (Faraday’s law).
The polarity of the voltage is such that a current is generated on closing a circuit whose induced magnetic field opposes the original magnetic flux, i.e. it tends to reduce the magnetic field (Lenz’s rule – Figure 1.).
Taking a winding with N turns, Faraday’s law can be expressed in the following form.
A = cross section of the coil
l = length of the coil or of the magnetic circuit
I = current through the coil
L = inductance of the coil [H(enry) = Vs/A]
So the inductance limits the change in current once a voltage is applied. It can be calculated from the coil data:
The energy stored in the magnetic field is subject to the following relationships:
The energy stored in the volume V is composed of both the magnetic field strength H and the magnet flux density B. For transformers and chokes with ferromagnetic cores, the flux density is limited by saturation and is constant throughout the magnetic circuit. If an air gap is introduced (material with permeability μ~1), the field strength is highest in this air gap with H = B/μ. It follows that the energy density is highest in the air gap. One also speaks of the energy being stored in the air gap.