Application of Johnson’s approximation in finite element modeling for electric field-dependent materials give improved understanding of voltage dependence and provide a method to help guide the design of future dielectric materials for MLCCs with improved performance.
Researchers from Department of Material Science & Engineering, University of Sheffield, Sheffield, UK in their article published by Applied Ceramic Technology Journal used Johnson’s approximation in a finite element code to simulate the electric field dependence of a core–shell microstructure material.
Abstract
We show how the microstructure, based here on a 50:50 volume fraction, influences the measured effective permittivity as a function of applied voltage. Using a Johnson’s parameter of β = 1.0 × 1010 Vm5/C3, verified from commercial BaTiO3-based multilayer ceramic capacitors (MLCC), we show how the microstructure and the difference in core and shell conductivities alter the local fields generated and how this influences the voltage dependence of the effective permittivity. (class II MLCC DC BIAS impact)
Systems that comprise a conductive core-like material surrounded by a resistive shell experience little or modest voltage dependence due to the shell material providing shielding to large electric fields within the cores. Conversely, if the core material is more resistive than the shell material, substantial voltage dependence occurs with simulations showing over a 50% decrease in the effective permittivity. These simulations give improved understanding of voltage dependence and provide a method to help guide the design of future dielectric materials for MLCCs with improved performance.
Results and Discussions
These studies show that a key parameter in determining the core material change is the surrounding material’s conductivity. Used cases show significant sensitivity to the global electric field if the core material is lower or equal in conductivity to that of the shell.
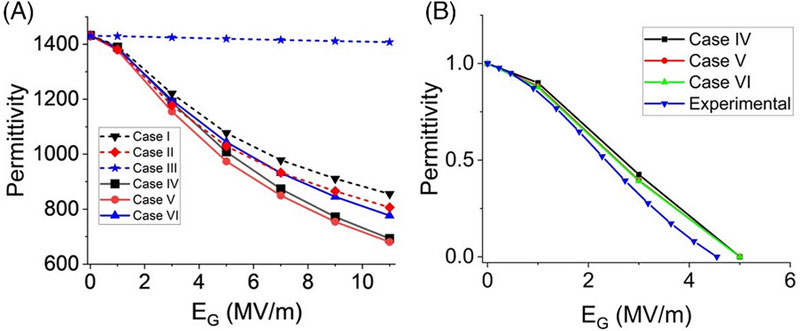
In Case I, the conductivity of the materials is identical and as such the electric field set up in both materials is the same. This leads to the system responding with a permittivity change in the core due to the applied global field.
In Case II, as the conductivity of the core is lower than the shell, an enhanced current density is generated in the core region. This leads to an enhanced electric field in the core and as such greater VCC sensitivity. In these configurations, it offers the ability to tune the capacitance and as such TCC through the control of dielectric layer thickness. This could be detrimental, however, as the increased local electric field could raise the likelihood of the core material failing and the possibility of dielectric breakdown.
While Cases IV and V have the same material properties as Cases I and II, although the shell is now field sensitive they still behave similarly. In Case IV, where the materials have the same conductivity, the shell VCC response now causes the overall permittivity to drop. This is also true of Case II but with a reduced amount due to the current mostly acting through the core and avoiding, if possible, the more resistive parallel shell regions lowering the electric field in those regions.
If the core is surrounded by a lower conductive material, such as Case III, the current primarily wants to find the path of least resistance through the core. This generates a higher electric field in the shell material, primarily in the top and bottom layers. This effectively “screens” the core from high local electric fields causing the system to exhibit almost little or no NFD.
Only a small region of the model, primarily the top and bottom surfaces of the core, experiences a high local field whereas the rest of the core material remains unchanged. This leads to the capacitance remaining relatively constant when increasing the global electric field and therefore reducing the system’s apparent sensitivity to field effects.
If the shell material is assigned field dependence as in Case VI, while the shielding effect to the core is still present, the shell material now experiences a drop in permittivity instead. Although this drop in Case VI is much stronger than in Case III, it is still less than that experienced by Cases IV and V. It can be seen that after normalizing the plot for permittivity, all plots, regardless of their VCC strength, they all experience the same general trend. It also shows that the experimental data follow a similar rate of drop in permittivity as the model data for Cases IV, V, and VI as the voltage is increased to 5 MV/m.
| Case | Core/shell | Permittivity | Conductivity (µS/m) |
|---|---|---|---|
| I/IV | Shell | 1000 | 100 |
| Core | 2000 | 100 | |
| II/V | Shell | 1000 | 100 |
| Core | 2000 | .1 | |
| III/VI | Shell | 1000 | .1 |
| Core | 2000 | 100 |
The studies shown here investigate how large changes in permittivity and conductivity of those regions affect the response; however, small changes (∼10% variation) in either the core or shell conductivity caused less than a 5% change in the overall field dependence response. It is only when the values start to become comparable (less than two orders of magnitude) that the current paths through the system are altered and then begin to affect the observed field dependence. We note, however, that the changes to the β value do influence the response more significantly, mainly as it is a scaling component of Equation, but the trend of the models, irrespective of the value used, remains the same.
Through the models presented here, we have assigned a 50:50 volume ratio for the core and shell materials. The measured strength of the VCC dependence of the system will be modified by the core–shell volume ratio due to changes in the current and field profiles previously shown by Heath et al. For example, if the volume fraction of core material were made larger and more conductive, a greater flow of current through the core would be expected, thereby raising the electric field. This would lead to a lower shielding effect and a greater field dependence to be exhibited. Other effects present in MLCC materials, such as grain shape, roughness, or porosity, have been shown to increase local electric fields and along with volume fraction are the focus of on-going and future studies.
Conclusion
In conclusion, we have developed a finite element modelling approach that can aid the understanding of how VCC is affected by the electric microstructure of a system. Typically, MLCC materials are formed from a BaTiO3 material with a doped shell, giving rise to a core that has higher conductivity than the surrounding shell.
The findings in this article indicate in this case over 80% of the core volume experiences a field that is lower than the global value applied and as such the core response is relatively unchanged. If the shell has little or NFD, then the apparent VCC change is negligible; however, if the shell does possess some field dependence, although the field which the core experiences is still reduced, a VCC reduction is observed and attributed to the change in the properties of the shell.
Therefore, through a selection of the core and shell properties, the VCC effects can be enhanced or suppressed as desired while still shielding the core from the high electric fields and improving the apparent breakdown strength of the system. These simulations provide an improved understanding of voltage dependence and help guide the design of future materials for MLCCs with improved performance.
Read the full scientific paper: Application of Johnson’s approximation in finite element modeling for electric field‐dependent materials – D’Silva Green – International Journal of Applied Ceramic Technology – Wiley Online Library