Published in Nature magazine, Yokouchi et al. researchers report a quantum-mechanical inductor, called an emergent inductor, that uses the electric field produced by the current-driven dynamics observed for intricate structures of magnetic moments (spins) in a magnet. Inductors are hard to miniaturize because their effectiveness is proportional to their size. An approach based on quantum mechanics could overcome this issue, offering many potential applications.
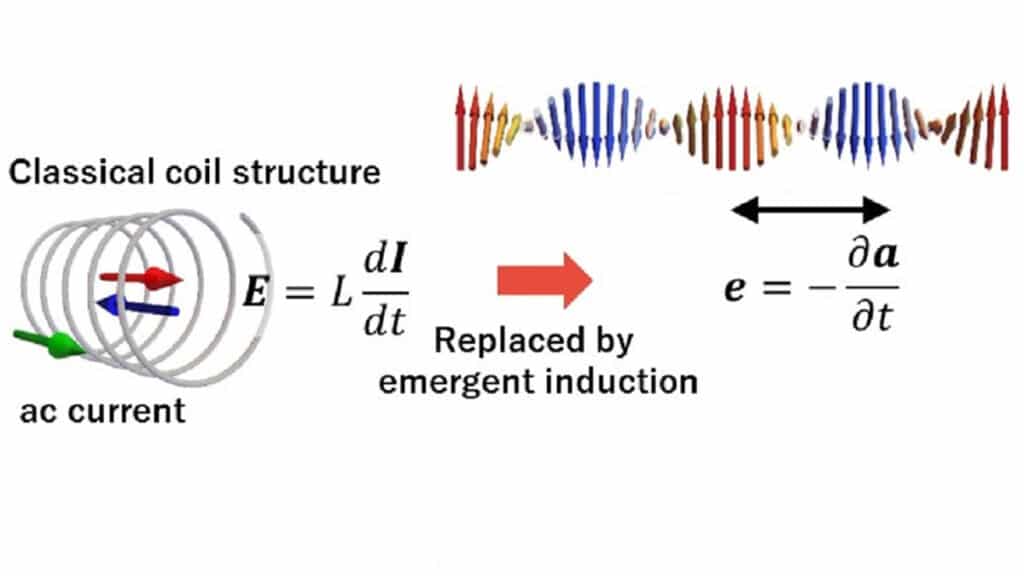
One of the fundamental components of electrical circuits is the inductor, which provides inductance (opposition to changes in electric current). Conventional inductors consist of a coil of wire wrapped around a central core. Unfortunately, because the inductance of such devices is proportional to their cross-sectional area, it is difficult to miniaturize them while keeping a reasonably high inductance. Yokouchi1 et al. report a quantum-mechanical inductor, called an emergent inductor, that uses the electric field produced by the current-driven dynamics observed for intricate structures of magnetic moments (spins) in a magnet. Notably, this device has an inductance that is inversely proportional to its area and does not require a coil or a core — characteristics that are highly desirable for practical applications.
Emergent electromagnetism refers to electromagnetism in which the generated electric and magnetic fluxes are described by a concept in quantum mechanics called a Berry phase2. Physical systems that exhibit emergent electromagnetism include magnetic systems that have non-collinear spin structures, whereby the direction of magnetization varies with the position of the spins. When electrons flow along such structures, they can become strongly coupled to the local arrangement of spins and acquire a Berry phase. This phase then acts as an effective electromagnetic field, termed an emergent field3.
For instance, an emergent magnetic field arises when electrons flow through what are known as topological non-collinear spin structures, those with a particular topology that makes them robust against small distortions or perturbations. The generated magnetic field leads to an extra signal in voltage measurements — known as Hall measurements — that is induced by a physical phenomenon called the topological Hall effect4,5. Given the complex nature of such spin structures, this voltage signal offers a convenient way to explore topological magnetic states in a wide range of materials6,7.
By contrast, an emergent electric field arises from the dynamics of non-collinear spin structures. For example, such a field is generated when a magnetic field drives the motion of domain walls8 — the boundaries between domains that have different magnetization orientations in magnetic materials. In 2019, it was shown theoretically that an emergent electric field could also be produced by the current-driven dynamics of non-collinear spin structures9. More spectacularly, it was predicted that this field would generate an inductance that is proportional to the rate of change of the current density. Because this density would be inversely proportional to the cross-sectional area of the device, the emergent inductance would increase with decreasing area, in sharp contrast to the situation in ordinary inductors (Fig. 1).
Yokouchi and colleagues exploited this idea using a micrometre-scale magnet made of Gd3Ru4Al12 (Gd, gadolinium; Ru, ruthenium; Al, aluminium) that contains various non-collinear spin structures, such as helical, conical and fan-shaped structures. They selected this material because it has a weak magnetic anisotropy (directional dependence of magnetic properties), and because its spin structures have a short pitch (spatial periodicity). Spins can move relatively freely under a weak magnetic anisotropy, and the emergent inductance is inversely proportional to the pitch length9.
The authors investigated the emergent inductance of their inductor using a technique called lock-in detection. They controlled the spin-structure state of the device by altering the temperature and strength of an applied magnetic field, and carried out measurements on different states. They also varied the length, width and thickness of the device, to confirm reproducibility and exclude the possibility that the observed signal was caused by external factors, such as the presence of contact electrodes.
Most strikingly, Yokouchi et al. observed a large emergent inductance (approximately –400 nanohenries), comparable to that of a conventional inductor, for a device of about one-millionth the volume of such an inductor. By changing the spin-structure state of the device, the authors clarified the correspondence between the emergent inductance and the non-collinearity and dynamics of the spin structures. This correspondence is well explained by the previously mentioned mechanism for emergent inductance.
For example, Yokouchi and colleagues discovered that the current-driven dynamics of the helical spin structures are responsible for the large emergent inductance. By contrast, the fan-shaped structures yield a much lower inductance because their local angular variations are much smaller than are those of the other structures. Moreover, the authors found that the sign of the emergent inductance can be switched between positive and negative by controlling the direction of spin-structure motion, also in striking contrast to ordinary inductors.
Yokouchi and colleagues’ work is important for several reasons. First, it offers a scalable approach for developing miniaturized high-inductance inductors, which could be used in many micro- or nanoscale electronic devices and integrated circuits. Such inductors would also be much simpler in design than are conventional inductors, because a coil and a core would not be needed. Second, the work opens up exciting opportunities for constructing highly efficient hybrid spin–electronic circuits and systems. And third, it serves as proof that a fundamental concept in quantum mechanics — a Berry phase — can lead to real-world applications.
However, practical uses of such emergent inductors will need further breakthroughs. One major challenge is to develop inductors that act at room temperature, rather than at the current temperatures of about 10 kelvin. Overcoming this limitation will require extensive exploration of potential materials, especially to find a magnet in which short-pitch non-collinear spin structures can be readily stabilized and manipulated at room temperature. Developing a scheme for adding these inductors to integrated circuits will also be essential for applications. Nevertheless, Yokouchi et al. have made a key discovery that could lead to future engineering efforts in electronic devices, circuits and systems, while establishing an inspiring bridge between the world of quantum mechanics and modern electronics.
Nature 586, 202-203 (2020) doi: 10.1038/d41586-020-02721-7
References
- 1.Yokouchi, T. et al. Nature 586, 232–236 (2020).
- 2.Berry, M. V. Proc. R. Soc. Lond. A 392, 45–57 (1984).
- 3.Xiao, D., Chang, M.-C. & Niu, Q. Rev. Mod. Phys. 82, 1959–2007 (2010).
- 4.Neubauer, A. et al. Phys. Rev. Lett. 102, 186602 (2009).
- 5.Schulz, T. et al. Nature Phys. 8, 301–304 (2012).
- 6.Vistoli, L. et al. Nature Phys. 15, 67–72 (2019).
- 7.Kurumaji, T. et al. Science 365, 914–918 (2019).
- 8.Yang, S. A. et al. Phys. Rev. Lett. 102, 067201 (2009).
- 9.Nagaosa, N. Jpn. J. Appl. Phys. 58, 120909 (2019).