Source: EDN article
by Bertram Schott & Adrian Michael.
Wirewound power resistors are usually rated with respect to continuous power, which can be insufficient for e-mobility applications. A typical application is the pre- and discharge of large capacitors, often referred to as “soft start.” In this case the pulse-handling capability of the resistor is also very important. This capability can be determined over a large range of pulse durations by combining theoretical basics with finite element simulations of the respective thermal performance. The results can be generalized so that changing customer specifications can quickly be evaluated and suitable resistors suggested.
Wire allows for pulse load
Wirewound power resistors are typically specified according to their continuous power rating. However, the resistive element, the wire, can pick up a relatively large amount of energy while undergoing only a moderate temperature rise due to its relatively high mass and heat capacity. This is why wirewound power resistors are the perfect choice for pulse load applications.
Specification of the pulse load capability is important
The specification of the pulse load capability is becoming increasingly important due to the widespread use of frequency and voltage converters. The pulse load capability is often only exemplarily documented by the specification of one pulse of a certain power or energy and duration. It is rarely specified by listing a table of a few pulse amplitudes and durations. Should the resistor be stressed by a pulse for a duration that is not in the range of those given in the datasheet, and which is not in the range of adiabatic boundary conditions, then it is difficult to calculate the maximum permissible pulse load. However, a combination of theoretical basics and finite element simulations allows for calculating the thermal performance of a resistor over a virtually unlimited pulse duration interval, i.e. from very short pulses to continuous power.
e-mobility needs pulse load capability
Limiting the charge and discharge current of capacitors is a typical application for wirewound power resistors in the e-mobility sector because of the respective high pulse load. Soldering all electrical components to a PCB may be preferred instead of using “external” resistors, in order to keep the production process as simple as possible. In this case a number of smaller wirewound power resistors are directly soldered to the PCB, replacing a single large wirewound power resistor. For that type of application and manufacturing, Vishay has put the focus on the AC-AT series [1], which is the first of its kind to be AEC-Q200 automotive qualified.
Pulse load generates heat
We look at the cooling of a resistor in order to be able to evaluate the effect of an electric pulse load. An effective way to do that is to presume that Newtonian cooling prevails, i.e. that the rate of temperature change is proportional to the temperature difference of the hot resistor and its cooler ambient materials, and that the temperature of the latter is constant. In the case of a cemented wirewound resistor (e.g. of the AC-AT series), that ambient material is the cement surrounding the wire. However, the following reasoning can be applied to enameled or sand-filled wirewound resistors, too.
Pulse load at adiabatic boundary conditions
Presuming Newtonian cooling, and hence the proportionality of temporal temperature change and maximal temperature of the wire or resistor, results in an exponential function describing the time-dependent temperature of the wire and resistor [2].
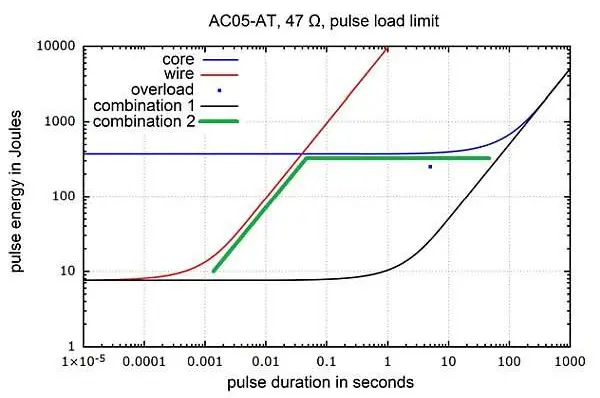
Figure 1 Pulse load limits for the ceramic core of an AC05-AT (blue curve) and the resistive wire for R = 47 Ω (red curve). Both curves are often combined: Combination 1 (black curve) underestimates the permissible overload (blue dot); Combination 2 (green line) overestimates the pulse load limit around the shown kink (at about 0.05 s).
The respective pulse load limits of the ceramic core of an AC05-AT 47 Ω resistor and its wire are shown in Figure 1 in blue and red, respectively. The maximal pulse load capability of the entire resistor is typically a simple combination of both curves. One way is an exponential function of the Newtonian cooling type, combination 1 in Figure 1, which is however far below the specified overload rating of 10 times the nominal power for 5 seconds and is therefore underestimating the pulse load capability in this range of pulse durations. Another way, combination 2 in Figure 1, overestimates the pulse load capability around the shown kink (at about 0.05 s), because the heating of the ceramic core is not taken into account when calculating temperature limits for the wire.
Finite-element (FE) simulation of pulse load
Delayed heating of the entire AC05-AT resistor under pulsating electrical load can easily be visualized by the heat flow and temperature distribution within the resistor by means of FE simulations. The resistive wire heats up during the pulse and then cools down. All other parts of the resistor are heated by that heat pulse with some delay. The duration of the pulse load does not matter in an FE simulation, as long as the boundary conditions are appropriately set. Therefore, the temperatures of the resistor and wire can be simulated for virtually any pulse duration, from adiabatic from the viewpoint of the wire (ms range) to almost continuous load of the resistor (100 s range). Consequently, the maximal permissible electrical pulse load can be determined by specifying a maximal permissible temperature of the wire.
Generalization by scaling
The results of a number of FE simulations can be generalized with respect to pulse duration by scaling with the characteristic time of thermal diffusion of the wire. This allows for the determination of a correction factor, which can be put into the exponential function, giving the temperature according to Newtonian cooling.
Pulse load at non-adiabatic boundary conditions
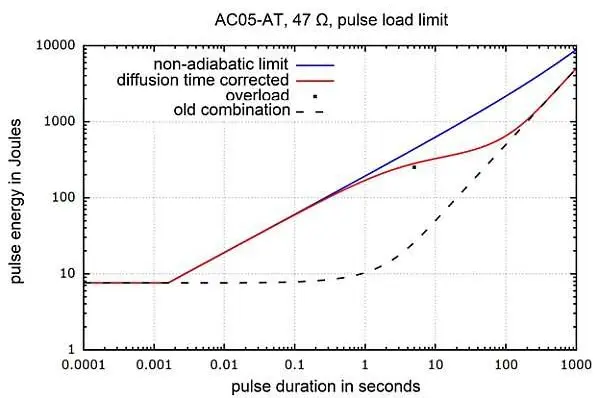
Figure 2 Maximal permissible pulse load for non-adiabatic boundary conditions from the viewpoint of the wire (blue curve) and corrected for the appropriate characteristic time of thermal diffusion (red curve). The usual limit curve with significant underestimation of the pulse load capability for pulse durations ranging from about 0.1 s to 10 s is shown for reference (black dashed line).
The above-mentioned correction factor allows for calculating the pulse load limit for non-adiabatic boundary conditions from the viewpoint of the wire (Figure 2, non-adiabatic limit). It does not yet converge to the pulse load limit of the entire resistor for long pulse durations though. However, if the characteristic time of thermal diffusion of the entire resistor is used for scaling at relatively long pulse durations, then the non-adiabatic limit curve converges to the limit curve for continuous load (Figure 2).
Application to other resistance values and resistors
The results of the FE simulations of the thermal behavior of a specific resistor (here the AC05-AT with 47 Ω) can be generalized by proper scaling. This allows them to be applied not only to all resistance values (wire configurations) available for the AC05-AT, but to all other AC-AT types, because they are of similar construction.
This method can even be applied to all other similar types of resistors, e.g. the G200 series [3], without additional FE simulations, and it is therefore extremely efficient. The advantage for the customer is that questions about pulse load capability can be answered in a timely and competent fashion.
References
- Cemented leaded wirewound resistors, AC, AC-AT, Vishay
- Bertram Schott, Estimating the pulse performance of wirewound power resistors, VDE Proceedings of PCIM Europe 2017, Nuremberg, Germany, May 2017.
- Axial Vitreous Leaded Wirewound Resistors, G200