This article describes dielectric constant and dissipation factor DF of plastic polymer materials, how to calculate it and factors affecting it.
What is Dielectric Constant?
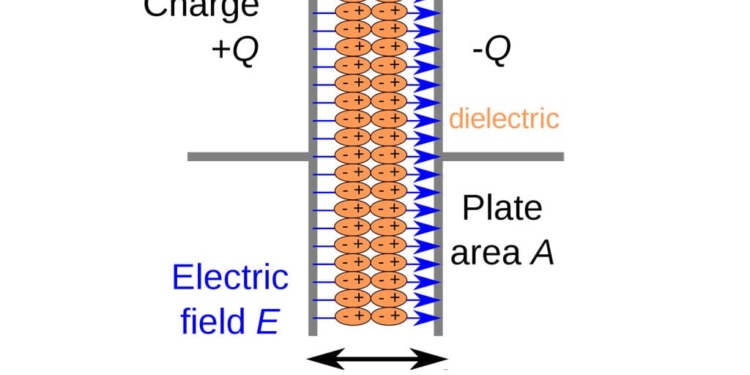
The dielectric constant (Dk) of a plastic or dielectric or insulating material can be defined as the ratio of the charge stored in an insulating material placed between two metallic plates to the charge that can be stored when the insulating material is replaced by vacuum or air. It is also called as electric permittivity or simply permittivity.
And, at times referred as relative permittivity, because it is measured relatively from the permittivity of free space (ε0).
Dielectric constant characterizes the ability of the material to store electrical energy.
Typical values of ε for some referenced and organic dielectrics are:
| Material | Dielectric Constant (ε) |
| Vacuum | 1.000 |
| Dry Air | 1.0059 |
| Foam Polyethylene | 1.6 |
| Fluoropolymers | 2.0 |
| Polypropylene | 2.1 |
| Butyl Rubber | 2.3 |
| SBR | 2.9 |
| Silicone Rubber | 3.2 |
| Plexiglass | 3.4 |
| PVC | 4.0 |
| Glass | 3.8-14.5 |
| Distilled Water | ~80 |
A dielectric constant of 2 means an insulator will absorb twice more electrical charge than vacuum.
Applications include:
Use of materials in the production of capacitors used in radios and other electrical equipment. Commonly used by circuit designers to compare different printed-circuit-board (PCB) materials.
Development of materials for energy storage applications.
For example, polymer-based dielectric composites are highly desirable for applications ranging from electronic packaging, embedded capacitors, to energy storage. These composites are highly flexible with a low process temperature and they exhibit a relatively high dielectric constant, low dielectric loss, high dielectric strength.
How to Calculate Dielectric Constant?
In other words, dielectric constant can also be defined as the ratio of the capacitance induced by two metallic plates with an insulator between them, to the capacitance of the same plates with air or a vacuum between them.
An insulating material with higher dielectric constant is needed when it is to be used in E&E applications where high capacitance is needed.
If a material were to be used for strictly insulating purposes, it would be better to have a lower dielectric constant.
The dielectric constant formula is:

Where:
- C = capacitance using the material as the dielectric capacitor
- C0 = capacitance using vacuum as the dielectric
- ε0 = Permittivity of free space (8.85 x 10-12 F/m i.e. Farad per metre)
- A = Area of the plate/sample cross section area
- T = Thickness of the sample
Dielectric Constant Units: This electrical property is a dimensionless measure.
The most generally used standard tests to calculate dielectric constant for plastics are ASTM D2520, ASTM D150 or IEC 60250 (ofcourse there exist several other methods as well, but they are not discussed here).
The method includes:
A sample is placed between two metallic plates and capacitance is measured. A second run is measured without the specimen between the two electrodes. The ratio of these two values is the dielectric constant. The test can be conducted at different frequencies, often between the 10Hz and 2MHz range
- The sample must be flat and larger than the 50mm (2 in) circular electrodes used for the measurement.
The other parameter of key importance apart of the dielectric constant is how much energy is lost inside the material during the current flow. This defines efficiency and usability of such material for the application at the given frequency range. The losses are expressed usually by DF dissipation factor that is more elaborated in article here: Dissipation Factor of Plastic Materials Explained and also add in the table below.
Polar Plastics Vs Non-polar Plastics
Dielectric properties of a polymer largely depend upon their structure. The structure determines whether a polymer is polar or non-polar and this in turn decided the electrical properties of the polymer.
- In polar polymers (PMMA, PVC, Nylon, PC etc.), dipoles are created due to imbalance in the distribution of electrons. These dipoles tend to align in the presence of electric field. Hence, this creates dipole polarization of the material making these materials only moderately good as insulators.
- While non-polar polymers (PTFE, PP, PE, PS) have symmetrical molecules and are truly covalent. There are no polar dipoles present in them and hence in presence of electric field does not align the dipoles. However, slight electron polarization occurs due to the movement of electrons in the direction of electric field, which is effectively instantaneous. These polymers have high resistivities and low dielectric constant.
Polar plastics have a tendency to absorb moisture from the atmosphere. Presence of moisture raises the dielectric constant and lowers the resistivity. With rise in temperature, there is faster movement of polymer chains and fast alignment of dipoles. This invariably raises the dielectric constant values for polar plastics.
Non-polar plastics are not affected by moisture and rise in temperature.
Factors Influencing Dielectric Constant
- Frequency – Dielectric constant decreases abruptly as frequency increases
- Moisture &Temperature
- Voltage
- Structure & morphology (see polar plastics vs non-polar plastics)
- Presence of other materials in the plastic
- Weathering and Deterioration
Dielectric Constant (ε) and DF Values of Several Plastics
| Polymer Type | ε Min | ε Max | DF Min | DF Max |
|---|---|---|---|---|
| ABS – Acrylonitrile Butadiene Styrene | 2.70 | 3.20 | 50 | 190 |
| ABS Flame Retardant | 2.80 | 3.00 | 70 | 90 |
| ABS High Heat | 2.40 | 5.00 | 20 | 350 |
| ABS High Impact | 2.40 | 5.00 | 20 | 350 |
| ABS/PC Blend – Acrylonitrile Butadiene Styrene/Polycarbonate Blend | 2.90 | 3.20 | 70 | 200 |
| ABS/PC Blend 20% Glass Fiber | 3.10 | 3.20 | 20 | 90 |
| Amorphous TPI Blend, Ultra-high heat, Chemical Resistant (Standard Flow) | 3.50 | 3.50 | 0.001 | 0.001 |
| ASA – Acrylonitrile Styrene Acrylate | 3.30 | 3.80 | 90 | 340 |
| ASA/PC Blend – Acrylonitrile Styrene Acrylate/Polycarbonate Blend | 3.00 | 3.40 | 20 | 190 |
| ASA/PC Flame Retardant | 3.20 | 3.20 | 110 | 170 |
| CA – Cellulose Acetate | 3.00 | 8.00 | 100 | 1000 |
| CAB – Cellulose Acetate Butyrate | 3.00 | 7.00 | 100 | 400 |
| CP – Cellulose Proprionate | 3.00 | 4.00 | 60 | 300 |
| CPVC – Chlorinated Polyvinyl Chloride | 3.00 | 6.00 | 100 | 200 |
| ECTFE | 2.57 | 2.59 | 130 | 170 |
| ETFE – Ethylene Tetrafluoroethylene | 2.60 | 2.60 | 6 | 100 |
| EVA – Ethylene Vinyl Acetate | 2.50 | 3.00 | 130 | 1000 |
| EVOH – Ethylene Vinyl Alcohol | 4.80 | 5.60 | 1800 | 2200 |
| FEP – Fluorinated Ethylene Propylene | 2.10 | 2.10 | 7 | 7 |
| HDPE – High Density Polyethylene | 2.30 | 2.30 | 3 | 20 |
| HIPS – High Impact Polystyrene | 2.40 | 4.80 | 4 | 20 |
| HIPS Flame Retardant V0 | 2.00 | 3.00 | 5 | 50 |
| LCP – Liquid Crystal Polymer | 3.30 | 3.30 | 20 | 20 |
| LCP Glass Fiber-reinforced | 3.00 | 4.00 | 40 | 40 |
| LCP Mineral-filled | 3.00 | 5.90 | 60 | 300 |
| LDPE – Low Density Polyethylene | 2.30 | 2.30 | 70 | 280 |
| LLDPE – Linear Low Density Polyethylene | 2.30 | 2.30 | 3 | 4 |
| MABS – Transparent Acrylonitrile Butadiene Styrene | 2.80 | 3.00 | 2.8 | 3 |
| PA 11 – (Polyamide 11) 30% Glass fiber reinforced | 4.80 | 4.80 | 0.03 | 0.03 |
| PA 11, Conductive | 3.00 | 9.00 | 0.05 | 0.25 |
| PA 11, Flexible | 3.00 | 9.00 | 0.05 | 0.25 |
| PA 11, Rigid | 3.00 | 9.00 | 0.05 | 0.25 |
| PA 12 (Polyamide 12), Conductive | 3.00 | 9.00 | 0.05 | 0.25 |
| PA 12, Fiber-reinforced | 3.00 | 9.00 | 0.05 | 0.25 |
| PA 12, Flexible | 3.00 | 9.00 | 0.05 | 0.25 |
| PA 12, Glass Filled | 3.00 | 9.00 | 0.05 | 0.25 |
| PA 12, Rigid | 3.00 | 9.00 | 0.05 | 0.25 |
| PA 46 – Polyamide 46 | 3.40 | 3.80 | 190 | 600 |
| PA 46, 30% Glass Fiber | 4.00 | 4.60 | 23 | 90 |
| PA 6 – Polyamide 6 | 4.00 | 5.00 | 100 | 600 |
| PA 6-10 – Polyamide 6-10 | 3.00 | 4.00 | 400 | 400 |
| PA 66 – Polyamide 6-6 | 4.00 | 5.00 | 100 | 400 |
| PA 66, 30% Glass Fiber | 3.50 | 5.60 | 100 | 1500 |
| PA 66, 30% Mineral filled | 4.00 | 5.00 | 200 | 1500 |
| PA 66, Impact Modified, 15-30% Glass Fiber | 3.40 | 4.20 | 130 | 200 |
| PA 66, Impact Modified | 2.90 | 5.00 | 100 | 2000 |
| PAI – Polyamide-Imide | 3.90 | 7.30 | 60 | 710 |
| PAI, 30% Glass Fiber | 4.20 | 6.50 | 220 | 500 |
| PAR – Polyarylate | 3.30 | 3.30 | 20 | 200 |
| PBT – Polybutylene Terephthalate | 2.90 | 4.00 | 10 | 200 |
| PBT, 30% Glass Fiber | 3.00 | 4.00 | 20 | 120 |
| PC (Polycarbonate) 20-40% Glass Fiber | 3.00 | 3.50 | 9 | 75 |
| PC (Polycarbonate) 20-40% Glass Fiber Flame Retardant | 3.00 | 3.80 | 9 | 100 |
| PC – Polycarbonate, high heat | 2.80 | 3.80 | 69 | 100 |
| PC/PBT blend, Glass Filled | 3.30 | 3.90 | 100 | 200 |
| PCTFE – Polymonochlorotrifluoroethylene | 2.00 | 3.00 | 10 | 250 |
| PE – Polyethylene 30% Glass Fiber | 2.70 | 2.80 | 20 | 80 |
| PEEK – Polyetheretherketone | 3.20 | 3.20 | 30 | 30 |
| PEEK 30% Carbon Fiber-reinforced | 3.20 | 3.40 | 29 | 32 |
| PEEK 30% Glass Fiber-reinforced | 3.30 | 4.20 | 20 | 20 |
| PEI – Polyetherimide | 3.10 | 3.20 | 13 | 25 |
| PEI, 30% Glass Fiber-reinforced | 3.00 | 4.00 | 15 | 53 |
| PEI, Mineral Filled | 3.00 | 4.00 | 10 | 15 |
| PEKK (Polyetherketoneketone), Low Cristallinity Grade | 3.30 | 3.30 | 0.004 | 0.004 |
| PESU – Polyethersulfone | 3.50 | 4.10 | 10 | 140 |
| PESU 10-30% glass fiber | 4.20 | 4.30 | 70 | 100 |
| PET – Polyethylene Terephtalate | 3.00 | 4.00 | 20 | 200 |
| PET, 30% Glass Fiber-reinforced | 3.00 | 4.00 | 120 | 1680 |
| PETG – Polyethylene Terephtalate Glycol | 3.00 | 4.00 | 20 | 300 |
| PFA – Perfluoroalkoxy | 2.10 | 2.10 | 2 | 2 |
| PI – Polyimide | 3.10 | 3.55 | 18 | 50 |
| PMMA – Polymethylmethacrylate/Acrylic | 2.00 | 5.00 | 200 | 200 |
| PMMA (Acrylic) High Heat | 3.20 | 4.00 | 400 | 600 |
| PMMA (Acrylic) Impact Modified | 2.90 | 3.70 | 300 | 400 |
| PMP – Polymethylpentene | 2.10 | 3.60 | 0.7 | 30 |
| POM – Polyoxymethylene (Acetal) | 3.30 | 4.70 | 50 | 110 |
| POM (Acetal) Impact Modified | 4.00 | 4.30 | 50 | 250 |
| POM (Acetal) Low Friction | 3.00 | 4.00 | 20 | 90 |
| PP – Polypropylene 10-20% Glass Fiber | 2.60 | 2.60 | 10 | 20 |
| PP, 10-40% Mineral Filled | 2.30 | 2.30 | 7 | 11 |
| PP, 10-40% Talc Filled | 2.30 | 2.30 | 7 | 11 |
| PP, 30-40% Glass Fiber-reinforced | 2.60 | 2.60 | 10 | 20 |
| PP (Polypropylene) Copolymer | 2.30 | 2.30 | 3 | 5 |
| PP (Polypropylene) Homopolymer | 2.30 | 2.30 | 3 | 5 |
| PP, Impact Modified | 2.30 | 2.30 | 3 | 5 |
| PPA – Polyphthalamide | 4.30 | 4.30 | 270 | 270 |
| PPA, 33% Glass Fiber-reinforced – High Flow | 3.70 | 3.90 | 0.014 | 0.016 |
| PPA, 45% Glass Fiber-reinforced | 4.40 | 4.60 | 0.9 | 0.2 |
| PPE – Polyphenylene Ether | 2.70 | 2.70 | 4 | 9 |
| PPE, 30% Glass Fiber-reinforced | 2.90 | 2.90 | 10 | 15 |
| PPE, Flame Retardant | 2.70 | 2.70 | 7 | 31 |
| PPS – Polyphenylene Sulfide | 3.00 | 3.30 | 4 | 30 |
| PPS, 20-30% Glass Fiber-reinforced | 3.30 | 3.80 | 10 | 32 |
| PPS, 40% Glass Fiber-reinforced | 4.00 | 4.00 | 13 | 20 |
| PPS, Glass fiber & Mineral-filled | 5.00 | 5.00 | 70 | 580 |
| PPSU – Polyphenylene Sulfone | 3.40 | 3.50 | 17 | 50 |
| PS (Polystyrene) 30% glass fiber | 2.50 | 2.50 | 5 | 28 |
| PS (Polystyrene) Crystal | 2.40 | 2.70 | 1 | 28 |
| PS, High Heat | 2.40 | 2.70 | 1 | 28 |
| PSU – Polysulfone | 3.00 | 3.20 | 8 | 64 |
| PSU, 30% Glass finer-reinforced | 3.60 | 3.70 | 40 | 60 |
| PTFE – Polytetrafluoroethylene | 2.10 | 2.10 | 2 | 2 |
| PTFE, 25% Glass Fiber-reinforced | 3.00 | 3.00 | 5 | 5 |
| PVC, Plasticized | 3.00 | 5.00 | 400 | 1600 |
| PVC, Plasticized Filled | 3.00 | 5.00 | 400 | 1600 |
| PVC Rigid | 3.00 | 4.00 | 60 | 200 |
| PVDF – Polyvinylidene Fluoride | 6.00 | 9.00 | 200 | 1700 |
| SAN – Styrene Acrylonitrile | 2.50 | 3.40 | 70 | 100 |
| SAN, 20% Glass Fiber-reinforced | 3.20 | 3.80 | 10 | 100 |
| SMA – Styrene Maleic Anhydride | 2.80 | 2.80 | 40 | 40 |
| SMMA – Styrene Methyl Methacrylate | 3.20 | 3.20 | 400 | 400 |
Find commercial grades matching your electrical property target using “Property Search – Dielectric Constant” filter in Omnexus Plastics Database.
Read more about plastic materials features:
- Flammability of Polymer Materials and UL94 Explained
- Coefficient of Linear Thermal Expansion on Polymers Explained