In this video prof Sam Ben-Yaakov provides an intuitive definition of the meaning of capacitance of non-linear voltage dependent capacitors such as ferroelectric-dielectric ceramic capacitors (Class II and Class III).
Introduction
Capacitance in voltage-dependent capacitors is a complex yet fascinating topic.
Unlike linear capacitors, where capacitance is straightforwardly defined as the ratio of charge (Q) to voltage (V), nonlinear capacitors—especially those using ferroelectric dielectrics, such as Class 2 and Class 3 ceramic capacitors—exhibit voltage-dependent behavior.
This article and video delves into the nuances of capacitance in these nonlinear capacitors, exploring their characteristics, measurement techniques, and practical applications.
Defining Capacitance
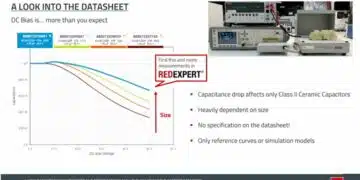
In linear capacitors, capacitance is simply calculated as Q/V, resulting in a linear Q-V relationship—a straight line. However, in nonlinear capacitors, this relationship becomes complex due to their voltage dependency. Manufacturers typically provide graphs showing capacitance as a function of temperature and voltage, derived from specific measurement setups.
- Total Capacitance: Defined as the ratio of charge to voltage at any given point. It’s represented as a straight line from the origin to a point on the Q-V curve.
- Local (Small Signal) Capacitance: Derived from the slope of the tangent at a given point on the Q-V curve. It reflects how the capacitance responds to small changes in voltage.
- Large Signal Capacitance: Relevant for large amplitude signals, defined as the ratio of change in charge to the change in voltage over a significant range.
Measurement Techniques
Capacitance measurements involve applying an AC excitation with or without a DC bias:
- With DC Bias: The bias is incrementally increased, and capacitance is measured at each step.
- Without DC Bias: The amplitude of the AC excitation is varied to observe changes in capacitance.
These measurements, typically conducted at 1 kHz, reveal how capacitance decreases as bias voltage increases—a key characteristic of ferroelectric capacitors.
Practical Applications
- Total Capacitance: Useful when analyzing charge transfer between nonlinear and linear capacitors.
- Local Capacitance: Crucial in circuits with DC bias and ripple voltage, such as buck converters.
- Large Signal Capacitance: Important for resonant converters and circuits with significant AC currents.
Energy Storage and Hysteresis
Energy stored in nonlinear capacitors deviates from the familiar ½CV² formula. Instead, it requires integrating the Q-V curve. Additionally, hysteresis effects—commonly observed in ferroelectric materials—may appear, though distinguishing true hysteresis from linear losses requires careful analysis.
Simulation Techniques
Using SPICE simulations, one can model the capacitance behavior based on manufacturer data. By digitizing the Q-V curve and integrating the small signal capacitance, the charge and energy stored can be accurately simulated.
Conclusion
Understanding the capacitance of voltage-dependent capacitors is vital for designing efficient electronic circuits. Through careful measurement, analysis, and simulation, engineers can optimize applications ranging from power converters to resonant circuits, leveraging the unique properties of nonlinear capacitors.