source: All about circuits article
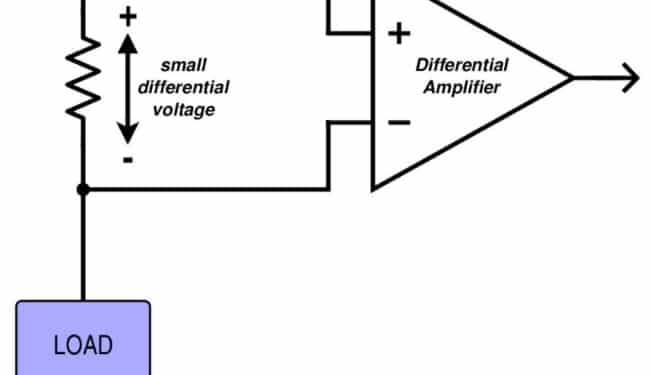
Despite the astonishing advancements in so many aspects of electronics technology, the dominant approach to measuring current is still based, as far as I can tell, on the use of a current-sense resistor. The resistor goes in series with the current-to-be-measured, the resulting voltage drop is proportional to the current, you measure the voltage, you divide by resistance, and you’re done. It’s a conceptually simple technique, but the details can be troublesome.
The “observer effect” tells us that any measurement will alter the state of the thing being measured. The change might be negligible or even undetectable, but it’s always there. So we know that any method of measuring any quantity in a circuit will have some effect on the state of the circuit. Nevertheless, the nature of electricity is such that we can often measure voltage without significantly altering the rest of the circuit. This “measurement-friendly” nature of potential difference makes current measurements look all the worse.
The Trade-Off
The fact is, the use of a current-sense resistor is an invasive technique. You’re deliberately adding resistance where previously you had only a conductor. Of course you can make the resistance very small, but this is a diminishing-returns situation: Yes, lower resistance is better (to a point), because you have less wasted power and the resistor more closely resembles the effect of a wire or PCB trace. But the whole point here is to generate a voltage that can be measured and converted into current. This voltage will be fed to an amplifier, and amplifiers come with fixed errors, i.e., errors that are not dependent on the amplitude of the input signal. Thus, smaller sense resistance means lower voltage, which means lower signal-to-noise ratio, which means lower accuracy in your current measurement.
Don’t forget to consider the less-effort-required solutions, such as the INA250 from Texas Instruments. It already has a sense resistor and probably works better than anything that I could design.
So as always, everything depends on your requirements and restrictions. You can combine a very-low-value resistor (say, 1 mΩ or less) with a high-precision amplifier and end up with fabulous current measurements and minimal effect on the original circuit. But, you might find that the current-sense circuit costs more than the rest of your device, or you might botch the PCB layout and thereby downgrade your accuracy from “fabulous” to, say, “above average.”
KOA Speer’s Contribution
My instinct tells me that 1 mΩ is a bit extreme for most applications, and that is reflected in the resistance range of KOA Speer’s UR73V2A series of current-sense resistors, which are available from 10 mΩ to 100 mΩ. The power rating is 0.5 W, and the package is 0805.
We often don’t have to worry about power dissipation with very-low-value resistors, but just in case you’re measuring high currents, remember to derate.
I think we all realize that precision is important when you’re choosing a current-sense resistor: you determine current based on the resistance; if the resistance in your calculation is different from the actual resistance, you have error. But another thing to keep in mind is the temperature coefficient.
Like just about everything else in a circuit, resistance is affected by temperature. This means that if your calculation uses a single value for the current-sense resistance, it will always be at least a little bit wrong, unless your device is designed to operate only in a temperature chamber. The easiest way to reduce this wrongness is to choose a resistor with a low temperature coefficient. The UR73V2A series comes with temperature coefficient as low as ±75 ppm/°C. The parts per million thing can be distracting, so let’s take an example.
Your device is sitting next to an oven which is now actively baking some French bread, and the operational temperature eventually increases by 20°C. This corresponds to 75 ppm/°C × 20°C = 1500 ppm, and (1500 ppm)/106 = 0.15%. This higher resistance will create a higher voltage drop, but your code still uses the original resistance, so your calculation will yield a current that is 0.15% higher than the actual current. I don’t know what your requirements are, but I’m guessing that most applications could cope with this sort of error.