source: EDN article
Rick Chapman -April 01, 2017 A recent design project called for a πΩ resistor. This new approach to creating nonstandard resistor values should find wide use in a range of applications.
I continue to design analog circuits just in case it turns out that computers are a passing fad. A recent design project called for a πΩ resistor, and I was surprised that I could not find one in current catalogs. Figure 1 shows how I created one by paralleling two 1% resistors, of 3.16 Ω and 536 Ω. This simple Design Idea results in a resistance value of 3.1415 ohms, exactly the design goal. This new approach to creating nonstandard resistor values should find wide use in a range of applications.

Figure 1 The synthesized πΩ resistor
Our new company, Transcendental Passives, has submitted patent applications for this two-resistor circuit, as well as an advanced three-resistor version. Our first product will be the πΩ resistor described here – a part that can be used in a variety of products, such as an electronic tape measure that reports the circumference of a circular object by measuring its diameter.
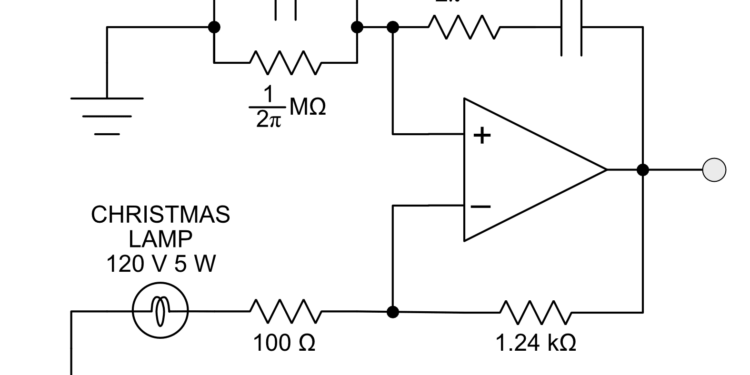
Our second product line will be resistors with values that are multiples of 1/2π. We think they will find wide use in RC oscillators designed to operate at integer frequencies. For example, Figure 2 shows a Wien-bridge oscillator designed to oscillate at exactly 10 Hz.

Figure 2 A precise 10Hz Wien-bridge oscillator
An e Ω resistor (2.718 Ω) is now on the drawing board, and should be useful in log amplifiers and timing circuits. The three-resistor prototype is shown in Figure 3, although laboratory testing of this circuit has not yet been completed. Notice that the extra complexity of the three-resistor circuit may be justified even for high-volume products because it can synthesize the desired resistance with lower precision, lower cost components.

Figure 3 The e Ω prototype
Our multi-year roadmap includes resistors with values of Planck’s constant (for the development of radars with a thermal noise floor (kTB) of 1), and Avogadro’s number, for weight scales that read out in number of atoms. Chip-scale versions of these products are also in the works. We think the basic concept can also be extended to capacitors, although the inductor market may be too small to support such advanced designs.