source: Power Electronics article
When modeling the dynamic behavior of power converters, ESR is important value because it predicts the output ripple of the converter as well as predicting capacitor lifetime.[2] Power dissipated in ESR causes the capacitor’s temperature to increase and its capacitance and lifetime to decrease.
A simple and direct method for measuring ESR is proposed in [3], in which the ESR is determined directly by the ratio of the capacitor’s ripple voltage to ripple current. But the implementation is quite expensive and troublesome. To determine ESR using only voltage measurements, Chen et al. [4] suggested that under some specific conditions, the inductor ripple current could be assumed to be constant and hence the output ripple voltage determines the ESR. However, the proposed method is limited and its precision is not high.
Here, we present a simple measurement technique for the determination of capacitor ESR.
Proposed Method:
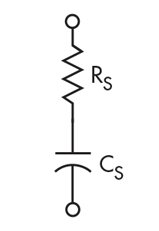
Assume a model like that shown in Fig. 1, for Capacitor Under Test (CUT):

1. Model of capacitor under test.
This model ignores lead inductance. Suppose that CUT is connected to a sine wave generator with frequency Fg and internal resistance rg, as shown in Fig. 2:

2. CUT connected to a sine wave generator.
The transfer function of this circuit is:

Equation 1, shows the high pass nature of this circuit. Therefore, we can approximate the transfer function as:

Equation 2 is the basis for our capacitor ESR measurement. When the input frequency is high enough we can simplify the input-output relation as algebraic Equation 2. For high frequencies, the circuit acts like an attenuator with the attenuation factor:

Measurement of circuit’s attenuation factor and generator’s internal resistance leads to rc, the capacitor’s ESR:

Instead of using a sine wave excitation, we can use a square wave. This allows us to use a Fourier series to write an equation with levels +Vm and -Vm, and period T:
Where:

A square wave consists of odd harmonics. When fundamental harmonic is high enough, a capacitor acts like short circuit and output voltage is approximately attenuated version of input voltage in steady state. Circuit attenuation in steady state is directly related to capacitor equivalent series resistance, rc , that can be obtained by measuring the circuit’s attenuation factor and using Equation 3.
Simulation Results:
Simulink diagram is shown in Fig. 3:

3. Simulation diagram of circuit in Simulink.
A square wave with amplitude +1 and -1 volt is used as excitation. Signal generator output resistance is taken as 50 Ω, capacitor is 30 μF with 0.8 Ω ESR. Steady-state output waveform is shown in Fig. 4:
4. Steady-state output of circuit.
The calculated attenuation factor of the circuit is:

and CUT’s ESR is calculated as:

Laboratory Results:
A signal generator with nominal 50 Ω output resistance provides the excitation. An output resistance of 47.1 Ω is measured with the aid of a simple voltage divider. Steady state output voltage peak-peak voltage is measured with the aid of a digital scope. Figure 5 shows s sample output.

5. Sample output voltage waveform.
Calculated ESR Values

This simple measurement technique provides accurate results and allows a more precise power converter model.
References
1. Amaral A.M.R., Cardoso A.J.M.: An experimental technique for estimating the ESR and reactance intrinsic values of aluminium electrolytic capacitors. Proc. Instrumentation and Measurement Technology Conf., IMTC 2006, April 2006, pp. 1820–1825.
2. Sankaran V.A., Rees F.L., Avant C.S.: Electrolytic capacitor life testing and prediction. Proc. 32nd Annual Meeting IEEE Industry Applications Society, October 1997, vol. 2, pp. 1058–1065
3. Venet P., Perisse F., El-Husseini M.H., Rojat G.: Realization of a smart electrolytic capacitor circuit, IEEE Ind. Appl. Mag., 2002, 8, (1), pp. 16–20
4. Chen Y.-M., Chou M.-W., Wu H.-C.: Electrolytic capacitor failure prediction of LC filter for switching-mode power converters. Proc. 40th Annual Meeting IEEE Industry Applications Society, October 2005, vol. 2, pp. 1464–1469.
5. Amaral A.M.R., Cardoso A.J.M.: An ESR meter for high frequencies. Proc. Int. Conf. on Power Electronics and Drives Systems, PEDS, 2005, pp. 1628–163
6. D.W. Hart, “Power electronics,” Mc Graw Hill, 2010.
7. N. Mohan,T. M. Undeland , W. P. Robbins, “Power Electronics: Converters, Applications and Design,” John Wiley and Sons, 2002.
8. R.W. Ericson, D. Maksimovic, “Fundamental of power electronics,” Springer, 2001.
9. A.M.R. Amaral, A.J.M Cardoso: “An ESR meter for high frequencies“. Proc. Int. Conf. on Power Electronics and Drives Systems, PEDS, 2005, pp. 1628–1633.
10. R. Chen, J.D.V. Wyk, S. Wang, W.G. Odendaal: Improving the characteristics of integrated EMI filters by embedded conductive layers. IEEE Trans. Power Electron., 2005, pp. 611–619.
11. A.M.R. Amaral, A.J.M Cardoso: An experimental technique for estimating the ESR and reactance intrinsic values of aluminium electrolytic capacitors. Proc. Instrumentation and Measurement Technology Conf., IMTC 2006, April 2006, pp. 1820–1825.