source: EDN article
A quartz crystal’s case will be stamped with the devices’ rated operating frequency, but that number is only an approximation to the real story which is that there is more than one crystal resonant frequency, even in the ideal case. (No pun intended.)
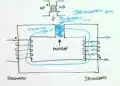
The following shows the equivalent circuit of an ideal crystal. There are only three circuit elements, an inductance L1 in series with a capacitance C1 and a second capacitance C2 in parallel with that L1 C1 series pair.

Figure 1 Equivalent Circuit of An Ideal Quartz Crystal.
There will be a series resonant frequency where the input impedance, Z, goes to zero where L1 and C1 are in series resonance. Capacitance C2 has nothing to do with that.
However, there is also a parallel resonant frequency where the input impedance, Z, goes to infinity. That is the frequency where C2 is in parallel resonance with the series combination of L1 C1 presenting an inductive impedance. That parallel resonance must occur at a higher frequency than the series resonance does in order to have the L1 C1 pair appear inductive at the parallel resonance.
Ergo, the parallel resonant frequency can ONLY be higher than the series resonant frequency, even if it’s only a teeny little bit higher. The parallel resonant frequency can NEVER be lower than the series resonant frequency. Which resonance will matter to you, if it does matter, will depend on the application.
Using a little algebra, the impedance Z comes to the following:

Figure 2 Impedance Equations
The series resonant frequency is Fseries = 1 / ( 2 * pi * sqrt ( L1 C1 ) )
The parallel resonant frequency is Fparallel = 1 / ( 2 * pi * sqrt ( L1 C1 C2 / ( C1 + C2 ) ) )

Figure 3 Relative Positions of Series and Parallel Resonances
featured image source: Kyocera