Understanding the input drive and full-scale range trade-offs in ADCs can be vital when designing analog receiver front ends, Rob Reeder, applications engineer, high-speed data converters, Texas Instruments published his article in Electronic Products Magazine.
Let’s face it: analog-to-digital converters (ADCs) operate differently. Their analog inputs are voltage-input-sensitive devices that leave radio-frequency (RF) engineers scratching their heads about how to match the ADC to the analog inputs.
Adding to this confusion, analog input interfaces are typically differential by nature and host a time-varying type of input impedance as the internal sampling switch opens and closes at the speed of light. This input impedance is thought to be a real resistive value across the ADC’s input bandwidth, but when plotted on a Smith chart, the trace curve just goes around and around.
In this article, I’ll look at some of the details related to analog input trade-offs, and how to properly deduce the ADC’s full-scale range in reference to the analog input network in dBm.
It’s all about headroom
Long ago, high-speed ADCs were designed on process nodes that supported voltage swings as large as 10-Vpp full scale.
They were even single-ended. Setting the ADC’s reference gave you some flexibility to make the full-scale range unipolar or bipolar.
Today, the process nodes are small – 65 nm or less – and the ADC’s internal analog input front end is biased at <2 V. This makes for significantly lower headroom, which can become a challenge when signal-chain designs need to interface with a 1- or 2-Vpp full-scale range, where the RF stops and the ADC begins.
Today, most high-speed ADCs employ differential inputs. This implies that you only have one-fourth the signal swing to wrap around the common-mode voltage (VCM) bias, or each analog input handles one-half the swing. Fig. 1 illustrates single-ended vs. differential signal properties and definitions

The ADC’s analog input VCM is important and needs to be satisfied by the external input network front end; otherwise, the device will have other performance challenges.
By dividing up the signal swing differentially, this interface enables you to maintain higher voltage levels across the full-scale range (that is, 1 or 2 Vpp); therefore, the differential nature of the analog input enables a smaller process node.
Full-scale trade-offs
Some ADCs are flexible and dedicate a few (out of the few thousand) serial peripheral Interface (SPI) registers in order to change the full-scale swing. Keep in mind that a design with a larger full-scale range generally yields a better signal-to-noise ratio (SNR). But better SNR performance usually decreases the harmonic performance of the spurious free dynamic range (SFDR).
The SNR increases because the signal swing can be larger now, assuming that the noise stays constant. Conversely, a smaller full-scale range enables better SFDR (HD2 and HD3); however, there is a slight sacrifice in SNR. See Figs. 2 and 3to understand these trade-offs.

As shown in Fig. 2, the input full-scale range changed from a default value of 800 mVpp to 430 mVpp. This reflects a slight increase in SFDR or HD2 and HD3. The input full-scale value changing from the default 800 mVpp to 1.0 Vpp yields a slight increase in SNR, as shown in Fig. 3. Notice the HD2 and HD3 decrease in Fig. 3 vs. Fig. 2.

In either case, you can “dial in” the best AC performance for your application by optimizing the full-scale value.
Other SPI registers allow you to change the input impedance, possibly halving or doubling the input impedance on the differential inputs. This means that you can optimize the “matching” network when designing the front end. The input full-scale range will once again change in value. Not all ADCs offer these features, but some do, which is easier than changing the front-end circuitry to accommodate different applications or adding additional components to the front-end network.
Full-scale breakdown
Let’s go through an example that illustrates the trade-offs involved when designing a high-speed matching network to the ADC. Baluns and front-end networks will add loss and additional noise figure to the overall signal chain, so it is pertinent to understand the input-drive trade-offs during the design and optimize the full-scale value. The input drive defines the amount of signal (in dBm) required to drive the converter at a full-scale range in front of the interface network – in this case, a passive balun network.
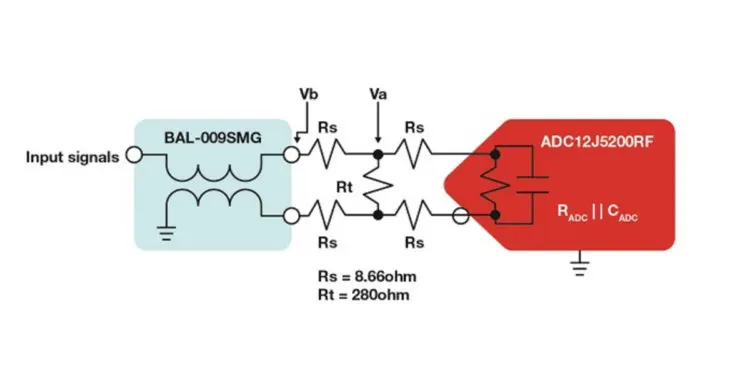
In the example, the ADC is the RF-sampling, 12-bit ADC12DJ5200RF from Texas Instruments and the balun is the BAL-0009SMG from Marki Microwave. A front-end resistive network interfaces the balun’s differential outputs to the ADC differential inputs. See Fig. 4.

Let’s do some calculations next. If you don’t have a dBm calculator handy, I recommend downloading the latest graphing calculator app to your phone.
The ADC12DJ5200RF has a default analog input full-scale range of 800 mVpp (Vfs) with a 100-Ω (RADC) differential load internally that is calculated in terms of dBm (Equation 1):
PADC= 10*log((Vfs/2/sqrt(2))2/Radc/1e03) or 10*log((800m/2/sqrt(2))2/100/1e-3) = -0.97 dBm (1)
Since the input network is differential, it can become a little difficult to crunch through the numbers. But by using the single-ended approach, the full-scale voltage at the input of the ADC has a value of 400 mVpp (Vfs/2) or -3.97 dBm.
By using a front-end resistive network as described above, you can calculate the voltage dividers to understand the losses required to achieve a 400-mVpp (Vfs/2) full-scale value.
RADC/2 = 50 Ω and Rs form a resistive divider or Va = (Vfs/2)*(((RADC/2)+Rs)/RADC) = 0.47 V, which gives you a single-ended voltage input at Rs and Rt.
Now, let’s calculate the single-ended voltage at the balun output (Equation 2):
Vb = Va*(((((RADC/2)+Rs)||(Rt/2))+Rs)/(((RADC /2)+Rs)||(Rt/2))) = 0.57 V (2)
You can make this single-ended voltage a differential voltage or 2*Vb or 1.13 V = Vdiffbo. The power at the balun’s output is then expressed as Equation 3:
Pbo = 10*log((((Vdiffbo/2/sqrt(2))2)/RADC)/1e-3) = 2.06 dBm (3)
Now for the fun part: Either consult the data sheet of the prospective balun or measure the balun on your nearest four-port vector network analyzer and take an SDS21. This will yield a single-ended-to-differential measurement and provide the correct insertion loss across the balun. In this example, measuring the BAL-0009SMG yields a loss of 4.2 dB at 1 GHz. See Fig.

Adding the balun losses to the output power found at the balun’s output (resistive network loss) determines what the input drive is: 2.06 + 4.2 or +6.26 dBm; +6.26 dBm is the required input amplitude required to drive the analog input signal on the primary of the balun to the full-scale range of the ADC.
Therefore, the total losses from top to bottom are 6.26 + 0.97, or a 7.26-dBm loss. Remember the PADC equation (with the result of -0.97 dBm) to achieve the full-scale value? Add that result back in, too.
A quick note on noise figure: When designing an analog receiver chain, the loss in the balun and front-end network counts as well. For this case, the noise-figure addition will be the loss found or 6.26 dBm, which is a value of 1.3 Vpp vs. the default full-scale value of 800 mVpp. This means 20*log(1.3/0.8) = 4.22 dB of additional noise figure in the receiver signal chain.
Now, let’s take a different approach: measuring it in the lab with the ADC12DJ5200RF evaluation module. Using the signal generator, dial in the output level until the ADC is very near the full-scale value at 1 GHz. In this case, the input full-scale value was +6.3 dBm from the signal generator reading. Keep in mind that balun variance and cable/connector losses can cause some differences. See Fig. 6.

Conclusion
Understanding the input drive and full-scale range trade-offs in ADCs can be vital when designing analog receiver front ends. The quick method given here for analyzing the front end should help keep trade-offs well within range. If you have any questions or feedback on this analysis, please comment below.
The author would like to dedicate this article to his mentors: James Bobis and Walt Kester.