source: Electronic Design article
Dan Harmon | Aug 11, 2017 Use a current-sense amplifier that integrates a precisely matched, resistive gain network to minimize the temperature-drift effects of the gain error.
As more systems become electrified, thermal management has turned into one of the “hottest” issues facing designers. Using current measurements for thermal management is a leading indicator of system performance and faults, whereas simply monitoring the temperature is potentially a lagging indicator. Accurately monitoring the current consumed, especially over temperature, has become vital as designers pack more functionality into tighter areas.
While room-temperature calibration tends to be relatively straightforward, performing multi-temperature calibration is time-consuming and costly. Identifying ways to minimize the effects of temperature on current measurements can improve system performance and minimize system design margins, as well as potentially lower the total cost of ownership (TCO).
Sources of Error in Current Measurements
As I stated in my September 2015 article, “Mitigate Error Sources to Maximize Current-Measurement Accuracy,” there are multiple contributing sources of error in current-measurement applications. In the article, I listed these sources of errors:
Amplifier-related errors:
- Input offset voltage (VOS) and VOS drift
- Common-mode rejection ratio (CMRR)
- Power-supply rejection ratio (PSRR)
- Gain error and gain drift
System errors:
- Gain-setting network tolerance, matching, and drift
- Printed-circuit-board (PCB) layout
- Shunt-resistor tolerance and drift
You can see that “drift” is part of four of the seven items on both lists, which emphasizes the importance of minimizing the additional errors caused by temperature in a current-measurement implementation.
Discrete Current-Measurement Implementations
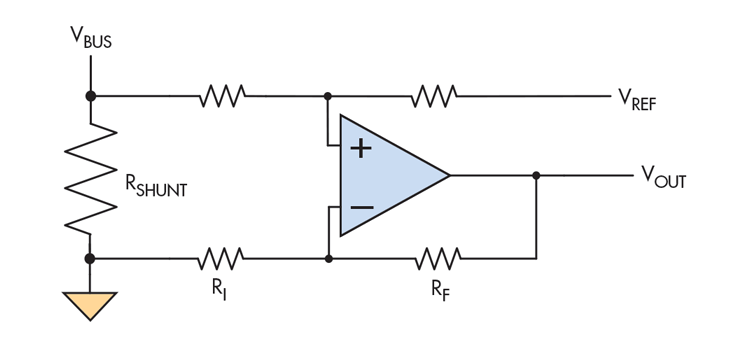
Many system designers choose a discrete amplifier and external gain network for their low-side current-measurement applications because it’s viewed as a low-cost alternative. There are two options when using a discrete circuit for low-side current sensing: a single-ended or differential configuration. Figure 1 shows the latter.

1. This basic differential amplifier configuration is used for current measurement.
In either configuration, the gain of the system is defined as G = RF/RI. The worst-case initial (or room-temperature) gain error is simply the tolerance of the discrete gain resistors. Assuming an application with a gain of 20, where RF = 100 kΩ and RI = 5 kΩ, Table 1 reveals how that looks for different resistor tolerances.

To understand the effects of temperature, let’s assume the same gain implementation with nominal resistor values and then apply various standard temperature coefficients (tempcos). Tempcos are usually specified in terms of parts per million per degree Celsius (ppm/°C). To get from ppm to a percentage, simply divide by 10,000. Table 2 shows the calculation results for a variety of resistor tempcos.

The issue here is that the drift could be in opposite directions and different for each resistor, which means minimizing these temperature effects in gain errors requires multipoint calibration (as well as temperature monitoring) to enable temperature compensation in the system management controller. The additional circuitry and resources (calibration means people and time!) can significantly drive up the TCO. Plus, as the tempcos drop, the resistor becomes more expensive, and in turn drives up the TCO.
Calibration
As I mentioned, performing system calibration can minimize (or even eliminate) initial errors. Typical calibration occurs at the total system level and involves two-point calibration. Performing two-point calibration enables you to minimize the error at both low current levels (due to the offset of the system), as well as at higher current levels where gain error is the primary error source.
A video training series from Texas Instruments titled “Getting Started with Current Sense Amplifiers,” beginning with session 2.1, discusses this topic in detail. Equation 1 describes the transfer function of the system:
VOUT = (IL × RSHUNT × G) + VOFFSET (1)
The intent of calibration is to identify the factors needed to correct for the amplifier’s offset voltage (VOFFSET), the gain error of the network (G), and the shunt resistor error (RSHUNT). Applying zero current calculates the necessary offset correction. Using a current close to the nominal load will calculate the total gain correction factor, accounting for both the shunt tolerance and amplifier gain network.
Minimizing the offset error is very straightforward—choose an amplifier with low VOS and low VOS drift. You will have to make a tradeoff between performance and cost. As discussed above, trying to perform two-point calibration at multiple temperatures to calculate the drift component of the offset error is costly and time-consuming.
Current-Sense Amps Integrate Precision Matched Gain Networks
Current-sense amplifiers are specialized integrated circuits designed specifically to measure current. As shown in Figure 2, these amplifiers have four fundamental benefits compared to a discrete implementation.

2. A current-sense amplifier offers several key benefits over a discrete current-sense implementation.
The benefit of the precision, matched gain-resistor network really manifests itself in how the gain error changes over temperature. The way the resistors are designed and fabricated on-chip enables near-perfect matching of both the initial error as well as the temperature drift. The absolute accuracy of the resistors isn’t a factor in minimizing gain error; what’s critical is how well they’re matched. If both RF and RI are off by 10% in the same direction (either plus or minus), then the ratio remains ideal and the gain error is zero.

3. This part of Texas Instruments’ INA180 product datasheet electrical specifications table shows offset and offset drift.
When a current-sense amplifier specifies a room temperature gain error of 1%, for instance, in Texas Instruments’ INA180 datasheet (Fig. 3), it’s actually an indicator of how well-matched the resistors are opposed to the external gain network, where 1% resistors result in ±2% error.

4. The plot compares approximate measurement error over temperature between a current-sense amplifier with 20-ppm/°C drift and a discrete implementation using a gain network with 50-ppm/°C resistors.
The drift is also typically low on the integrated resistors—20 ppm/°C in the case of the INA180, which minimizes the effect of temperature drift on the total error. Figure 4 approximates the impact on error for two different amplifier arrangements over temperature. For this comparison, make the following assumptions:
- An ideal 200-mΩ shunt with 0% error and no drift.
- Room-temperature calibration to eliminate the initial offset and gain network errors.
- Offset drift of 5 µV/°C for both configurations.
- Configuration No. 1 uses an external gain network of 20 V/V with a 50 ppm/°C gain network.
- Configuration No. 2 is a current-sense amplifier with matched resistors configured for a gain of 20 V/V and 20 ppm/°C drift.
Summary
Maximizing accuracy in current measurements over temperature is critical in many applications. While room-temperature calibration is relatively straightforward, performing multi-temperature calibration is time-consuming and expensive. Using a current-sense amplifier that integrates a precisely matched, resistive gain network will minimize the temperature-drift effects of the gain error.
Implementing a low-drift amplifier architecture allows you to minimize the offset error over temperature. On that front, Texas Instruments has developed zero-drift current-sense amplifiers, including the INA180 and INA181, that enable high initial room-temperature accuracy while minimizing the effects of temperature.