Analyzing the leakage current from capacitors in the circuit of smart devices and selecting alternative components to reduce leakage could allow smart devices to last longer.
The spread of the IoT has driven up demand for smart devices such as sensors or actuators that are self-powered or able to run for long periods up to several years from an energy source as small as a coin cell. The art of ultra-low-power design has quickly become extremely sophisticated, all the way from the energy-harvesting or battery-management system to the antenna, turning off any subsystems when not needed and getting the maximum from every joule.
Despite energy-conscious circuit and software design, capacitor leakage could thwart your struggle to make the available milliamp-hours last for long enough. Multiple capacitors are typically needed to stabilize the power from an energy-harvesting system, or DC/DC converter and when charged behave like leaky buckets that continually allow a small amount of charge to dissipate, wasting precious energy.
Although only a few microamps, the leakage current can be comparable to the amount you might go to great lengths to divert, say, from the microcontroller through intricate use of power-saving modes. It makes sense to analyze the leakage current from capacitors in the circuit and consider selecting alternative components to reduce it.
Opportunities for Savings
Figure 1 shows the reservoir capacitor network recommended for a PIR-sensor reference design published by TI, comprising five capacitors. Ten years’ maintenance-free operation is a common target for this type of product, but poorly selected capacitors could draw more current than the coin cell can deliver for 10 years.
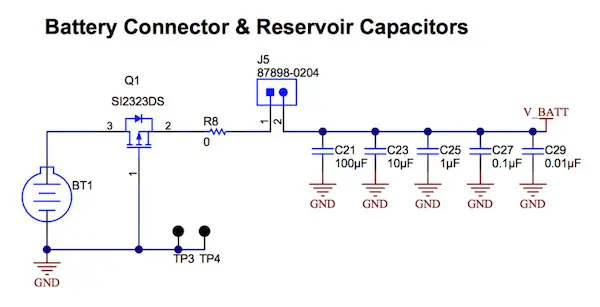
Figure 1. Battery energy can be lost through power-supply filtering and stabilization capacitors.
Similarly, in an energy-harvesting system, a large capacitance is needed to drive the application and is calculated according to the average power consumption. A small portion of the energy collected by the harvesting mechanism, such as a solar cell or Peltier module, is stored in the capacitors and lost as these discharge over time.
Technology Choices
Choosing the right technology, voltage rating, and capacitance value can make a huge difference in the amount of energy lost to leakage. Let’s take a look at ceramic capacitors (MLCCs), which are widely used to filter power-supply noise and provide hold-up energy to cover interruptions in power delivery or ensure shut-down can complete properly. Because the leakage current is small, the effect is quantified in terms of the device’s insulation resistance: a higher insulation resistance implies lower leakage.
The MLCC comprises multiple parallel plates separated by the ceramic dielectric. Generally, the highest possible capacitance value is desirable, in the smallest possible case size. Capacitor manufacturers have developed thin dielectric layers, fine particles, and precision lamination technologies to boost capacitance within the size constraints of standard SMD case sizes. On the other hand, thicker dielectric layers are needed to achieve a higher voltage rating: increasing the voltage rating increases the insulation resistance and hence reduces leakage, although capacitance is also lower if the case size remains the same.
We can see how the dielectric thickness, applied voltage, and electron mobility influence leakage current. The electric field within the capacitor exerts a force on charged particles:
F = E*q = U/d * q
This force drives the flow of electrons within the device, which constitutes the leakage current. For a given applied voltage, it is clear that the force F and therefore the leakage current will increase as the dielectric thickness, d, reduces.
Another way to relate capacitance to case size is through the equation:
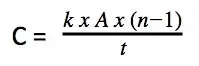
We can see that if we want to keep the same capacitance while decreasing the area (e.g. 0812 to 0402), then we can either reduce the dielectric thickness or increase the number of layers. The most likely approach is to use a combination of both. Overall, we can see that downsizing the capacitor inherently increases leakage.
We must also be aware of the change in leakage over temperature. As the mobility of charged particles increases with temperature, so, too, does the leakage. In practice, MLCC leakage increases by a factor of more than seven between room temperature and 45°C.
Calculating Leakage Current
Calculating the leakage current allows an assessment of its effect on battery runtime. Note that immediately after voltage is applied, the current initially flowing in the capacitor comprises the charging current and dielectric absorption currents, as well as the leakage current. As the charging current and absorption currents decay, the current flowing converges to the leakage current.
The datasheet for a ceramic capacitor states the guaranteed minimum insulation resistance, or insulation resistance limit, in Ohm-Farad (Ω-F), in terms of the case size and capacitance value. To calculate the insulation resistance for a given capacitor, simply look up the specified Ohm-Farad figure for the device and divide by the capacitance value. The leakage current at the working voltage can then be calculated by applying Ohm’s law:
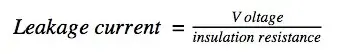
Consider this example, if using 10x 47µF commercial X7R MLCCs for power-rail filtering, at a working voltage of 5V. The datasheet guarantees an insulation resistance specification of 500MΩ.µF for this device:
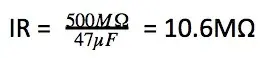
The DC leakage for the array of 10 capacitors can then be calculated:
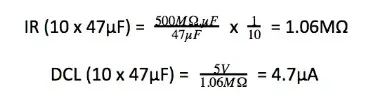
Tantalum Capacitors
Tantalum capacitors are characterized by high volumetric efficiency, low noise, and stability over time, making them an excellent choice for power-constrained IoT devices that are required to operate maintenance-free over an extended lifetime.
For these types of capacitors, assessing the DC leakage current is somewhat easier than for ceramic capacitors. The datasheet expresses the DC leakage current directly as a fraction of the capacitance value and voltage. For the KEMET T491 standard MnO2 capacitor series, this expression is:
DCL = 0.01 x C x V
Hence for 470µF capacitance with an applied voltage of 5V, comparable to the previous example, the DC leakage is:
DCL = 0.01 x C x V = 0.01 x 470 x 5 = 23.5µA
For the KEMET T489 series, which is engineered specifically for low leakage, the expression is:
DCL = 0.0075 x C x V = 0.0075 x 470 x 5 = 17.6µA
Hence, replacing T491 capacitors with 470µF of T489 devices can achieve a valuable reduction in leakage current.
In tantalum capacitors, the leakage current is heavily dependent on the ratio of rated applied voltage to rated voltage, due to the link between voltage rating and dielectric thickness. The graph of Figure 2 shows how leakage current is significantly reduced when the applied voltage is much lower than the rated voltage.
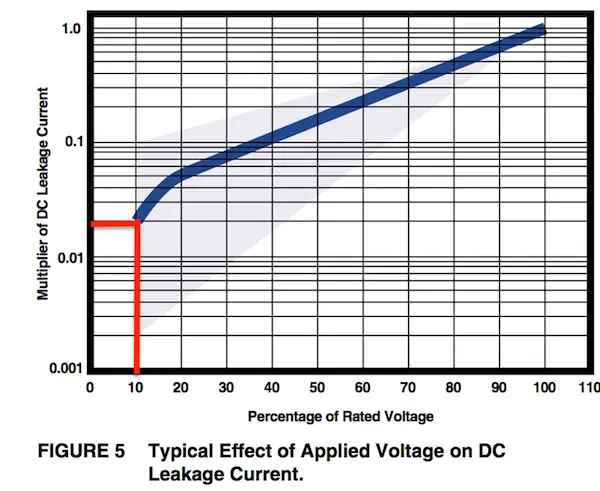
Figure 2. Typical variation of DC leakage with applied-voltage/rated-voltage ratio.
Specifying a capacitor with a rated voltage 10 times higher than the applied voltage can reduce the DC leakage by a factor of 50. Designers can take advantage of this in circuits where very low leakage current is required, at the expense of an increase in device size.
Note that leakage is also dependent on temperature so this, too, should be taken into account when calculating the effect on the system energy budget.
Capacitor DC Leakage is an Important Design Consideration
Capacitor DC leakage phenomenon is important to consider when designing ultra-low-power systems or devices that must operate for a long period without charging or replacing the battery. Examples include PIR sensors or energy-harvesting systems that require large capacitance to maintain a stable supply of energy to the system.
It is worth calculating the effect of leakage current on the energy budget for the system as a whole to determine any necessary mitigation. Ceramic capacitors with high capacitance values tend to have higher DC leakage. On the other hand, devices of higher voltage rating benefit from lower leakage but also have less capacitance in relation to package size. Leakage can be reduced by specifying capacitors from a dedicated low-leakage family, such as the T498 tantalum series.