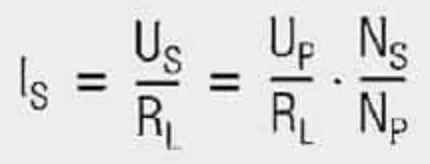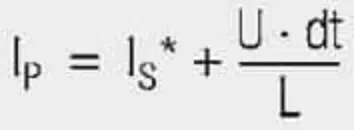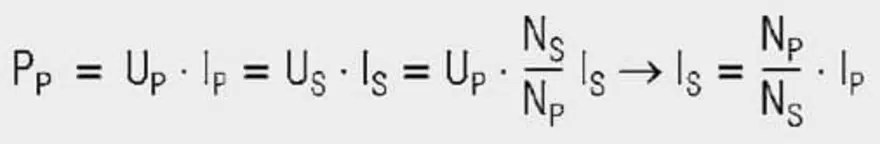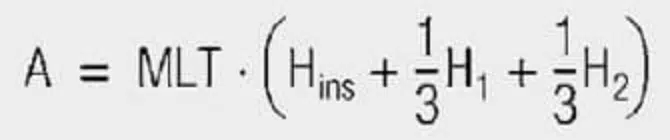This article explains the basic functionality and equations of transformer and solenoid.
Transformers
What is a transformer ?
A transformer is a device that transfers electric energy from one alternating-current circuit to one or more other circuits, either increasing (stepping up) or reducing (stepping down) the voltage.A transformer consists of at least two windings, with the winding turns NP on the primary side and NS on the secondary side.
For the sake of simplicity, we will look at an ideal transformer with a turns ratio of 1 : 1.
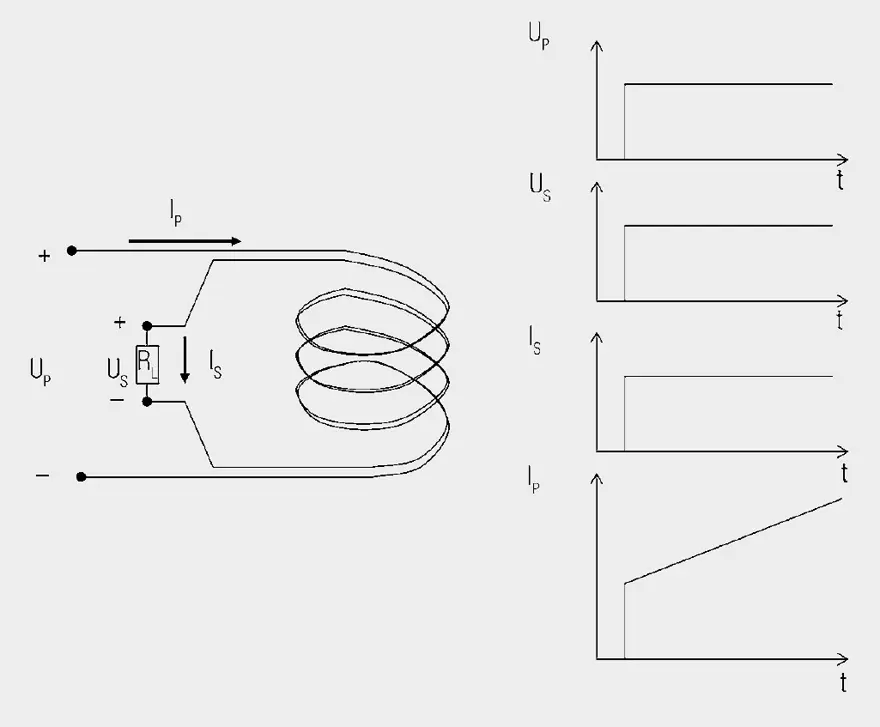
In a first step, we will look at a transformer with an open secondary winding NS (Figure 1.). A UP voltage pulse is created at winding NP. Due to the inductance of the winding, this pulse generates a linearly progressive current IP.
The following applies:
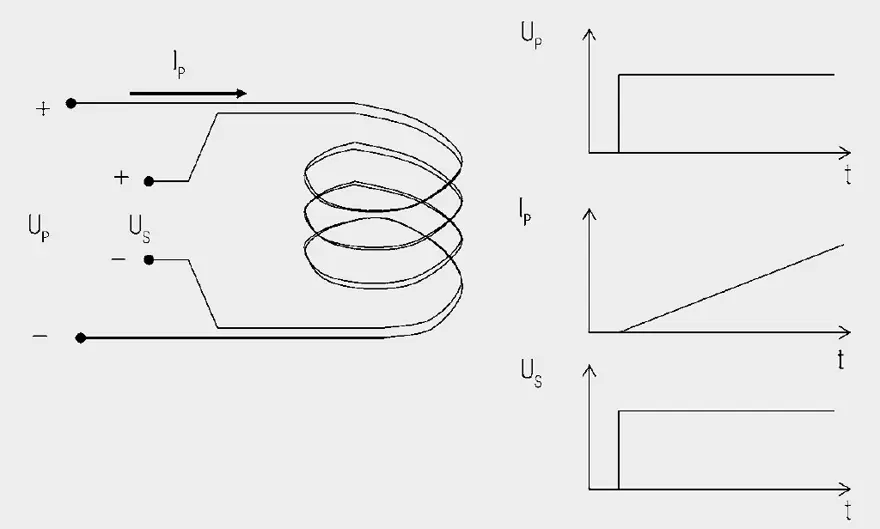
Winding NS also wraps around this magnetic flux. Changing the magnetic flux creates voltage.
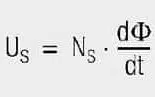
If you solve both equations after changing the voltage and then equate them, you will get the following for the voltage transformation expressed by eq. [3].
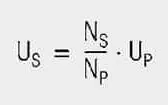
Current does not flow in winding NS because the winding is open. If we now connect winding NS to a load resistor RL (Figure 2.), the voltage induced in NS generates a current flow through the load resistor:
The primary current now consists of the transformed secondary current and the linearly progressive magnetisation current that is already available without load.
As no power can be generated, the transformed power is the same as the primary power put into the system. If the magnetisation current is disregarded, the following applies:
Currents are thus transformed in the reversed direction as voltage. The following also applies:
Resistances are thus transformed with the transformation ratio squared. This also applies to inductances, capacitances and impedances. So the magnetising current is not transferred to the secondary side. It is required to generate the magnetic field. The aim of the transformer design must therefore be to keep the magnetizing current as small as possible.
There are two possibilities here:
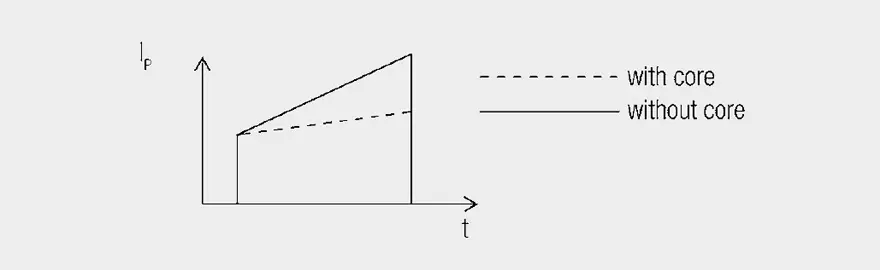
- Insertion of a highly permeable core to increase the primary inductance. This causes the magnetizing current to rise less steeply and is therefore smaller (Figure 3.).
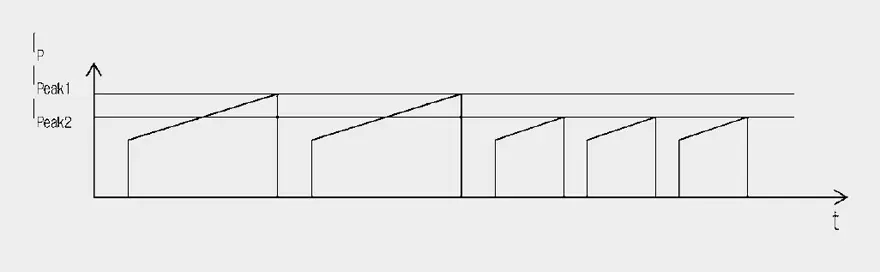
- Shorter voltage pulses with higher frequency are generated, as the rise in current stops at the end of the voltage pulse and starts again at the original point for the next pulse (Figure 4.).
Parasitic effects
In reality, there are other factors that affect the behavior of transformers. The most important ones are:
- Leakage inductance
- Coupling capacitance (capacitance between windings)
- Winding capacitance (capacitance within a winding)
Leakage inductance
Looking at two windings, we see that the entire flux is not coupled to the other winding. A part of the streamlines of the magnetic field closes outside of the other winding. This part of the inductance is called “leakage inductance.” To understand how to minimize leakage inductance, you must know the parameters that influence it.
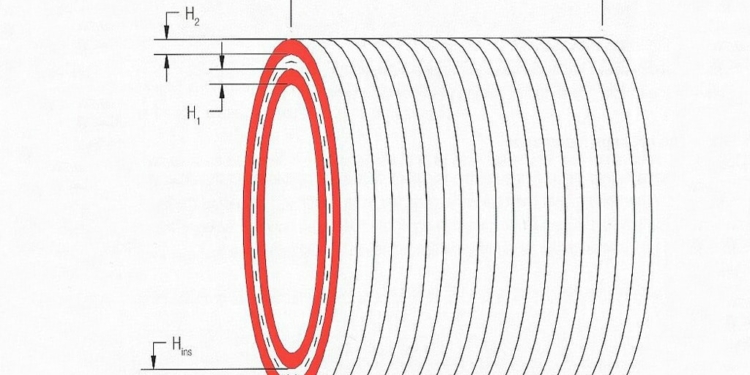
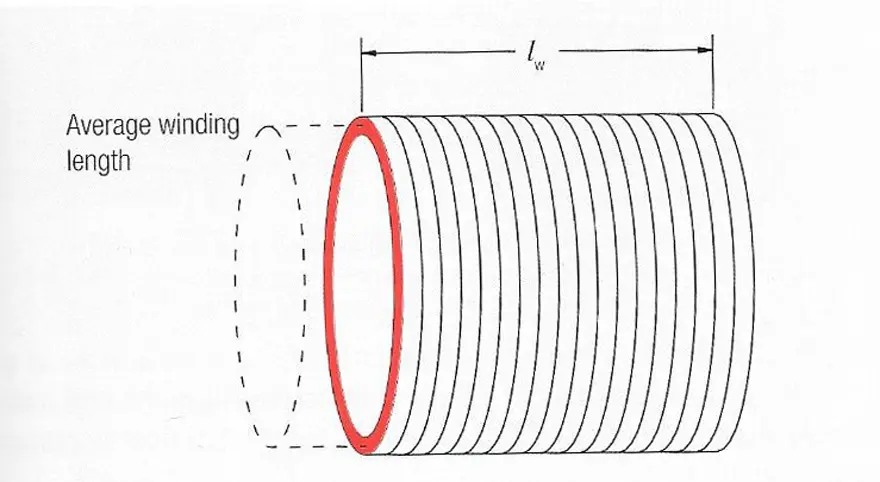
If you look at a long concentric coil (Figure 5.), its inductance results from:
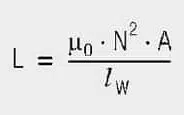
lW Length of the coil
N Winding turns
A Cross section of the coil
If a second winding is wound on top of it (Figure 6.), the leakage inductance results from eq. [6]
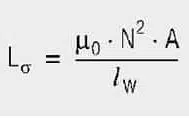
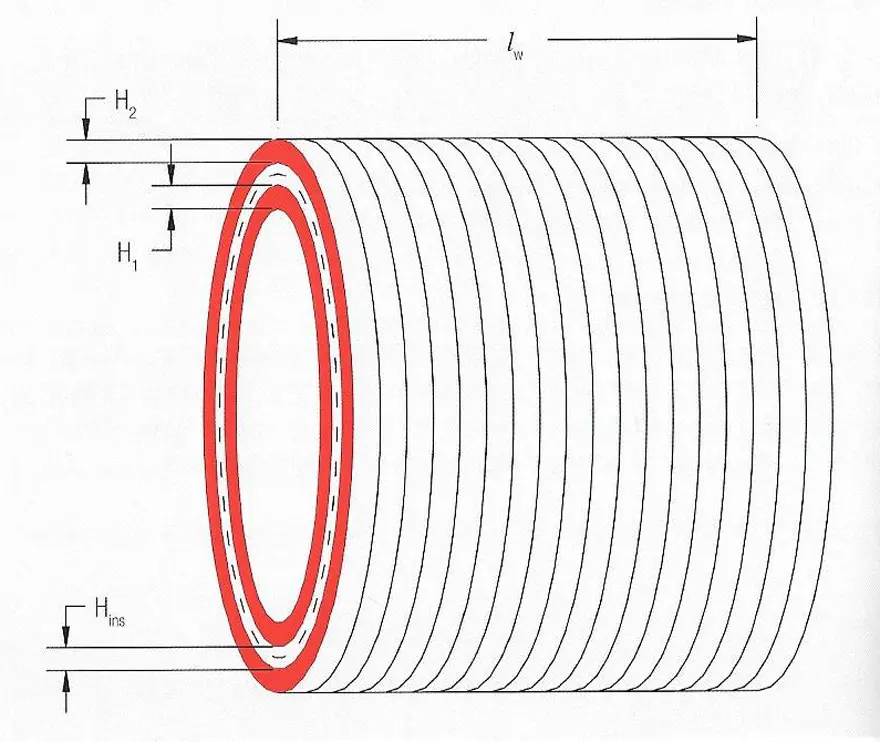
Where A here is the surface between the two windings. It can be calculated using:
MLT Mean length of turn
Hins Distance between the windings (isolation)
H1, H2 Winding height of windings 1 and 2
Coupling Capacitance
You can picture the coupling capacitance between the two windings as plate capacitor between the two windings. From this it follows that you can reduce this capacitance either by increasing the distance or reducing the surface. Both directly increase leakage inductance.
Winding Capacitance
Each winding builds up winding capacitance because they are isolated from each other and rest on different potential. This capacitance increases with the number of layers that are required within a winding. It can be reduced by means of various winding technologies, e.g. Z-wind (wire is returned after each layer).
For deep inside How Transformer Works see also video: How Transformer Works
Solenoids
Derived from two Greek words: Solen (pipe) and Eidos (coil), the solenoid is a type of an electromagnetic device that converts electrical energy into mechanical energy. It is generally made by tightly wounding wires in a helix shape around a piece of metal. Whenever an electric current passes through it, a magnetic field is created.
Working Principle
A solenoid works on electromagnetism and electromagnetic force. It consists of a round cylindrical coil that has several number of wire turns, and a metal rod inside the coil that is free to move. When an electric current is provided to the coil, a magnetic field is generated due to which the metal core or rod inside the coil gets attracted due to towards the direction where the magnetic flux is high. This electromagnetic effect in a solenoid enables any connected plunger or armature to move as per our need.
To increase the magnetic force produced in a solenoid coil, we will have to increase the number of turns, N and the current, I.
Types Of Solenoid

AC Laminated Solenoid
It has a very high initial attracting force and very short closing time. It is made with a laminated metal or insulated thin sheets that are individually ,assembled.

DC-C Frame Solenoid
As its name states, this solenoid is constructed in such a way that it has a letter ‘C’ like frame cover around the coil. This type is widely used in gaming machines.
DC-D Frame Solenoid
As its name says, this solenoid has a coil that is covered by two ‘D’ frames on two sides. This types is generally used in AC power applications.
Linear Solenoid

This type of solenoid has a freely movable steel or iron rod called plunger inside a round cylindrical shaped coil. The iron rod is allowed to freely move in or out of the cylindrical coil depending on the current applied.
Rotary Solenoid
It is a special type of solenoid where the magnetic force is converted into a rotational force or a rotary motion. It consists of an armature core mounted on a flat disk.
When a current is provided, the armature gets attracted towards the stator and the flat disk rotates.
Applications
Solenoid Valve

The solenoid valve is a simple device in which a solenoid is used for controlling and regulating the flow of fluid. It has a coil with free movable plunger or an iron rod with a spring inside it. When we energise the coil, the plunger moves from its position due to magnetic attraction and when we cut the power to coil, the plunger comes back to its original position with the help of a spring. As soon as the plunger comes in the path of the flowing fluid, its flow stops.

Solenoid Lock
Here we use the movement of solenoid plunger for the locking and unlocking mechanism. These solenoid locks are widely used in electronic and biometric password-based locks. It consists of a strong metal plunger that can move. When the coil gets magnetised due to an electric field, the plunger moves to perform the lock and unlock mechanism.
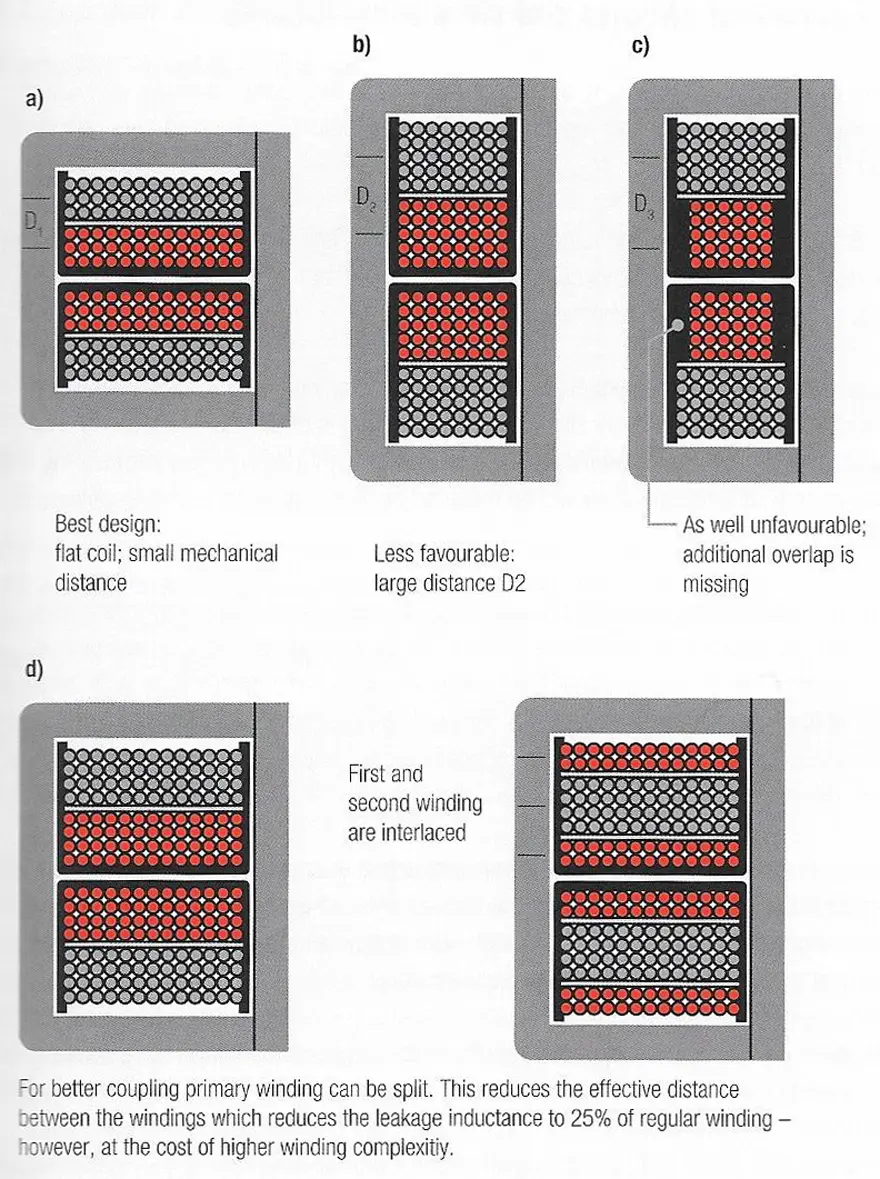
The leakage inductance is thus independent of core material and air gap. To minimize leakage inductance you must either increase the length of the coil (broad windings) or reduce the distance between the windings (e.g. bifilar wind).
Figure 7. shows various more or less ideal winding constructions. With existing geometry the most commonly used means is a sandwich construction (Figure 7.d), in which the secondary winding is wound between the primary winding that is divided into two halves. This doubles the length of the winding.