EMC Filters Design – from Component to Design

This article and Würth Elektronik webinar examines the fundamental principles of EMC filter design, from component-level characteristics through complete system integration, providing engineers with actionable insights for conducted emission mitigation in power electronics and communication systems.

The presentation deal with the following topics:

• The need for filters and different topologies
• Components and technologies
• Choosing components for a filter
• Design and simulation of filters
• How to destroy a filter

EMC Filters: From Component Selection to Practical Design

Electromagnetic compatibility (EMC) filter design requires systematic understanding of component behavior, filter topology, and practical implementation challenges.

1. Introduction

Electromagnetic interference (EMI) represents one of the most persistent challenges in modern electronic system design. As switching frequencies increase and circuit densities rise, conducted emissions from DC-DC converters, AC-DC power supplies, and high-speed digital circuits frequently exceed regulatory limits set by standards such as CISPR 22 and EN 55032

EMC filters are not merely collections of passive components enclosed in potting material; they are sophisticated frequency-selective networks whose performance depends critically on component selection, placement, and understanding of parasitic effects. A well-designed filter addresses both common-mode and differential-mode interference while maintaining signal integrity and meeting safety requirements.

This white paper presents a comprehensive approach to EMC filter design, drawing from practical engineering experience and measurement data to illustrate key principles. We examine why filters fail in real applications, how to select appropriate components based on frequency-dependent parameters, and proven techniques for optimizing filter performance.

2. Conducted Interference: Fundamentals and Frequency Ranges

2.1 Interference Mechanisms

Conducted electromagnetic interference propagates through electrical connections rather than radiating through space. The critical frequency boundary occurs at 30 MHz, below which cable-conducted emissions dominate, while above 30 MHz radiated emissions become significant. This transition reflects the wavelength relationship to typical conductor lengths in electronic systems.

For frequencies between 150 kHz and 30 MHz, regulatory testing focuses exclusively on conducted emissions measured at the equipment’s power input[page:1]. Efficient antenna formation requires conductor lengths approaching λ/4; below 30 MHz (λ > 10 meters), typical PCB traces and internal wiring remain electrically short, making radiation inefficient compared to conduction.

2.2 Common-Mode vs. Differential-Mode Noise

Understanding the distinction between common-mode and differential-mode interference is fundamental to effective filter design. Differential-mode noise appears as voltage differences between signal conductors, with currents flowing in opposite directions on line and return paths. Common-mode noise appears identically on all conductors relative to ground reference, with currents flowing in the same direction.

In power conversion applications, differential-mode currents typically originate from switching transitions in converter topologies, appearing at the fundamental switching frequency and harmonics. Common-mode currents arise from parasitic capacitances to ground and dV/dt across isolation barriers, manifesting predominantly at higher frequencies where capacitive coupling becomes significant.

Characteristic	Differential Mode	Common Mode
Current Direction	Opposite on line/return	Same direction on all conductors
Primary Frequency Range	Lower (fundamental and low harmonics)	Higher (parasitic coupling dominant)
Typical Amplitude	Larger (mA to A range)	Smaller (μA to mA range)
Primary Filter Component	X capacitors, differential chokes	Y capacitors, common-mode chokes

3. Filter Topologies and Component Placement

3.1 Basic EMI Filter Architecture

A practical EMI filter combines multiple filtering elements to address both interference modes. The canonical topology includes:

• Common-mode choke: Coupled inductor providing high impedance to common-mode currents while allowing differential signals
• Differential-mode chokes: Series inductors blocking high-frequency differential noise
• X capacitors: Line-to-line capacitors shunting differential-mode interference
• Y capacitors: Line-to-ground capacitors providing common-mode bypass paths

The effectiveness of each component varies dramatically with frequency and circuit impedance. X capacitors dominate differential-mode attenuation in lower frequency ranges, while Y capacitors become critical for common-mode suppression at higher frequencies.

3.2 Filter Order and Impedance Matching

Filter order, defined by the number of reactive components, directly determines the rejection slope: one reactive element provides 20 dB/decade attenuation, two elements yield 40 dB/decade, and three elements achieve 60 dB/decade. However, component placement relative to source and load impedance proves equally critical.

Starting with a series high-impedance element (inductor) works optimally when the source impedance is low, creating impedance mismatch that reflects noise back toward the source[page:1]. Conversely, starting with a shunt low-impedance element (capacitor) proves effective against high-impedance sources. The attenuation mechanism combines both dissipation in lossy components and reflection from impedance discontinuities.

The general design principle for maximizing filter effectiveness can be expressed mathematically as:

$$A_{\text{total}}=A_{\text{dissipation}}+A_{\text{reflection}}$$

where the reflection component depends on the impedance mismatch ratio:

$$A_{\text{reflection}}=20·\log {}_{10}(\left|\frac{Z_{\text{filter}}-Z_{\text{source}}}{Z_{\text{filter}}+Z_{\text{source}}}\right|)$$

4. Common-Mode Chokes: The Central Filter Component

4.1 Operating Principle and Magnetic Coupling

The common-mode choke represents the most sophisticated component in EMC filter design due to its ability to discriminate between wanted differential signals and unwanted common-mode noise. This selectivity arises from the magnetic coupling between windings on a shared ferromagnetic core.

Perfect symmetry between windings creates complete magnetic flux cancellation for differential-mode currents. When equal currents flow in opposite directions (differential mode), they generate magnetic fluxes of equal magnitude but opposite polarity, resulting in zero net core magnetization. Without core magnetization, no inductance appears, and differential signals pass with minimal impedance.

For common-mode currents flowing in the same direction, magnetic fluxes add constructively, saturating the ferromagnetic core and creating maximum inductance. This inductance generates high impedance that dissipates or reflects common-mode noise while allowing differential signals to pass unimpeded.

4.2 Core Materials and Frequency Response

Core material selection fundamentally determines the frequency characteristics of common-mode chokes. The complex permeability

$\mu =\mu ‘-j\mu ”$

describes both flux-conducting ability (real part of μ) and loss characteristics (imaginary part of μ).

Three primary material families serve different frequency ranges:

Core Material	Effective Frequency Range	Key Characteristics	Typical Applications
Manganese-Zinc Ferrite	10 kHz – 1 MHz	High permeability, moderate losses	Power supply filters, lower frequency EMC
Nickel-Zinc Ferrite	1 MHz – 100 MHz	Lower permeability, high losses	High-frequency EMC, RF suppression
Nanocrystalline	10 kHz – 10 MHz	Very wide bandwidth, excellent temperature stability, Curie temp >600°C	Wide-bandwidth filtering, harsh environments

For power inductor applications, engineers typically operate one decade below the resonant frequency to minimize core losses and maintain efficiency. EMC choke design inverts this principle: maximum losses occur precisely where filtering is required, making “poor” power inductor materials ideal for EMC applications.

4.3 Winding Styles and Parasitic Effects

Winding configuration significantly impacts both common-mode performance and differential-mode rejection. Two primary styles exist:

Bifilar winding: Both conductors wound together simultaneously, providing maximum symmetry and minimal differential-mode leakage inductance. The tight coupling results in excellent common-mode attenuation with negligible differential-mode impedance.

Sectional winding: Windings placed in separate sections of the bobbin, creating intentional asymmetry. This reduced symmetry generates significant leakage inductance, providing substantial differential-mode attenuation in addition to common-mode suppression.

The leakage inductance L_leak in sectional windings arises from imperfect magnetic coupling and can be estimated as:

$$L_{\text{leak}}\approx L_{\text{nominal}}·(1-k^2)$$

where k represents the coupling coefficient (k = 0.999 for bifilar, k ≈ 0.95-0.98 for sectional).

5. Component Selection Methodology

5.1 Beyond Inductance Value: Frequency-Dependent Parameters

Specifying a common-mode choke solely by inductance value (e.g., “1 mH”) provides insufficient information for filter design. The inductance measurement at low frequency (typically 1 kHz or 100 kHz) indicates only the initial slope of the impedance curve, revealing nothing about behavior in the critical EMC frequency range.

Effective component selection requires examining the complete impedance-versus-frequency characteristic, which encompasses:

• Low-frequency inductance region (inductive reactance dominates)
• Mid-frequency loss region (core losses create resistive impedance)
• High-frequency capacitive region (inter-winding capacitance creates resonance)

The impedance magnitude |Z| of a choke can be approximated across frequency as:

$$\left|Z\right(f\left)\right|\approx \sqrt{{2\pi f·L_{\text{eff}}}^2+{R_{\text{loss}}}^2}$$

where L_eff decreases with frequency as the core permeability drops, and R_loss increases due to core losses in lossy ferrite materials.

5.2 Rated Current and Thermal Considerations

The rated current specification for common-mode chokes reflects thermal limits rather than magnetic saturation. Manufacturers typically specify rated current as the DC current (flowing through both windings simultaneously) that produces a defined temperature rise, commonly 40K above ambient.

This measurement methodology ensures the rated value directly corresponds to application conditions. Derating curves extend operation to elevated ambient temperatures; for instance, operation at 90°C ambient might require derating to 80% of the rated current to prevent exceeding the maximum operating temperature of 125-140°C.

5.3 Saturation in Common-Mode Applications

Unlike differential-mode inductors, common-mode chokes exhibit negligible saturation concerns in typical applications. The field cancellation mechanism means differential-mode currents (which may be several amperes) do not magnetize the core significantly.

Common-mode currents remain in the microampere to milliampere range in properly designed systems. A choke might show 20% inductance loss (conventional saturation definition) at only 5 mA common-mode current, yet this poses no practical limitation since normal common-mode currents remain far below this level. Any system with multi-milliampere common-mode currents exhibits serious imbalance problems beyond simple EMC concerns.

6. Capacitor Selection and Safety Considerations

6.1 X Capacitors: Differential-Mode Filtering

X capacitors connect line-to-line (or line-to-neutral) and provide low-impedance shunt paths for differential-mode noise. Their effectiveness increases with frequency as capacitive reactance decreases according to:

$$X_C=\frac{1}{2\pi f·C}$$

X capacitor selection involves balancing several requirements:

• Capacitance value: Larger values provide better high-frequency attenuation but increase standby power consumption and discharge resistor losses
• Voltage rating: Must exceed peak line voltage with adequate safety margin
• Safety class: X1 (≤4 kV impulse) or X2 (≤2.5 kV impulse) classification per IEC 60384-14
• Discharge requirements: Regulations mandate X capacitors discharge to safe voltages (<50V) within specified times after disconnection, necessitating parallel discharge resistors

6.2 Y Capacitors: Common-Mode Filtering and Leakage Current

Y capacitors connect line-to-ground and provide essential common-mode noise bypass paths. However, their usage faces strict limitations due to safety ground leakage current concerns. Even at line frequency (50/60 Hz), Y capacitors conduct leakage current:

$$I_{\text{leakage}}=V_{\text{line}}·2\pi f·C_Y$$

where C_Y represents the total Y capacitance to ground.

Safety standards (IEC 60950, IEC 60065, IEC 60335) limit leakage currents to prevent shock hazards if ground connections fail. Medical equipment faces particularly stringent limits (typically <100 μA). These constraints restrict Y capacitor values, often limiting total Y capacitance to 2-4.7 nF for 230V applications.

Y capacitor safety classification (Y1, Y2, Y3, Y4) depends on insulation requirements and rated impulse voltages per IEC 60384-14. Class Y2 (≤5 kV impulse) serves most consumer and industrial applications, while Class Y1 (≤8 kV impulse) addresses reinforced insulation requirements.

7. Practical Filter Design Example: RS-485 Interface Protection

7.1 Design Requirements and Constraints

Consider designing an EMC filter for an RS-485 communication interface with the following specifications:

• Line impedance: 60Ω per conductor (120Ω differential)
• Maximum cable length: 1.2 km
• Signal bandwidth: DC to 15 MHz
• Required common-mode attenuation: Sufficient to meet EMC standards starting at 62.5 kHz
• Maximum acceptable differential-mode attenuation: 3 dB at 15 MHz

The 1.2 km cable length creates an efficient antenna at approximately 62.5 kHz (λ/4 ≈ 1200m for 62.5 kHz). Common-mode noise coupling to this cable antenna motivates the filter design.

7.2 Component Calculations

The 3 dB differential-mode attenuation limit at 15 MHz constrains the total differential-mode capacitance. For a π-filter topology with impedance Z₀ = 120Ω, the maximum differential-mode capacitance can be calculated from:

$$A_{\text{diff}}\left(\text{dB}\right)=20·\log {}_{10}(\left|1+\frac{Z_0}{2X_C}\right|)\le 3\text{ dB}$$

Solving for capacitance at f = 15 MHz:

$$C_{\text{diff,max}}=\frac{1}{2\pi f·Z_0({10}^{A/20}-1)}\approx 181\text{ pF}$$

This constraint must account for all differential-mode capacitances:

• X capacitors (intentional)
• TVS diode junction capacitance
• Y capacitor differential-mode component (Y capacitors exhibit differential-mode impedance despite ground connection)

For the example design, selecting X capacitors and considering parasitic contributions yields total differential-mode capacitance of 178 pF, safely below the 181 pF limit.

7.3 Simulation and Validation

LTSpice simulation using manufacturer-provided component models including parasitic elements produces attenuation curves closely matching measured filter performance. The simulation workflow includes:

1. Import component models with parasitic inductances, resistances, and capacitances
2. Construct filter schematic with appropriate source and load impedances
3. Perform AC analysis sweeping from 10 kHz to 100 MHz
4. Extract common-mode and differential-mode insertion loss
5. Compare simulation to measured performance using network analyzer

The design example achieved excellent agreement between simulation and measurement for differential-mode performance, with some deviation in common-mode response due to component tolerances and layout parasitics.

8. Common Filter Design Failures

8.1 Incorrect Component Placement

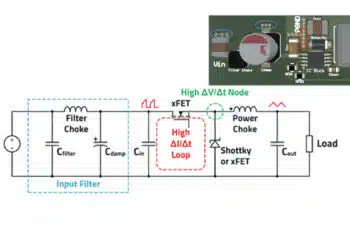
The most frequent filter failure mechanism involves improper placement relative to noise sources. Consider a typical power supply input path:

AC Inlet → Mains Switch → EMC Filter → AC-DC Converter

If the switch precedes the filter, the wiring between inlet and switch acts as an unfiltered noise coupling path. Inductive coupling between pre-filter and post-filter wiring creates a parasitic bypass around the filter’s high impedance, dramatically reducing effectiveness.

The coupling impedance Z_coupling between parallel conductors separated by distance d and with length l can be approximated as:

$$Z_{\text{coupling}}\approx j·2\pi f·M$$

where the mutual inductance M ≈ 0.2 × l × ln(d/r) nH for typical geometries. Even modest coupling creates low-impedance noise paths bypassing the filter.

Best practice: Place filters immediately at the enclosure entry point, keeping input and output wiring physically separated and minimizing parallel runs.

8.2 Filter Input/Output Feedback

Routing filter input and output conductors in parallel or in close proximity creates capacitive and inductive coupling that bypasses the filter’s intended isolation. This feedback mechanism effectively shorts out the filter at high frequencies where coupling impedances become significant.

Measurements show that parallel input/output routing can reduce filter effectiveness by 20-40 dB above 10 MHz. Orthogonal routing or physical shielding between input and output sections prevents this degradation.

8.3 Layout Parasitics

PCB trace inductance significantly impacts capacitor effectiveness. A capacitor intended to provide low-impedance shunt paths to ground becomes ineffective if connected through long traces whose inductive reactance dominates:

$$Z_{\text{total}}=j·2\pi f·L_{\text{trace}}+\frac{1}{j·2\pi f·C}$$

At the self-resonant frequency:

$$f_0=\frac{1}{2\pi \sqrt{LC}}$$

, the impedance reaches a minimum. Above f₀, inductive reactance increases and capacitor effectiveness degrades. A 1 nF capacitor with just 10 nH of trace inductance resonates at only 50 MHz, providing reduced bypassing at higher frequencies.

Mitigation strategies include:

• Minimizing trace lengths to bypass capacitors
• Using wide traces or planes for ground connections
• Placing capacitors as close as possible to connection points
• Employing multiple capacitors in parallel (different values) to extend frequency coverage

8.4 Incorrect Mode Filtering

Attempting to filter differential-mode noise with common-mode chokes, or vice versa, yields poor results. Some designers incorrectly substitute two separate inductors for a common-mode choke, expecting similar performance. However, uncoupled inductors provide only leakage inductance benefit (typically <1% of nominal inductance) for common-mode suppression, reducing effectiveness by 40 dB or more.

Proper filter design requires identifying the dominant interference mode through measurement (using current probes or LISNs) and selecting appropriate components.

9. Advanced Design Considerations

9.1 Complete Filter Solutions: CLFS Product Family

Integrated filter modules combine optimized component selection, controlled layout, and safety certifications in compact packages. These assemblies offer three primary topologies:

Single-stage: One common-mode choke, one X capacitor, two Y capacitors – basic filtering for lower attenuation requirements

Advanced single-stage: Additional X capacitor improves differential-mode performance without increasing volume significantly

Two-stage: Two common-mode chokes with intermediate and output X capacitors – maximum attenuation for demanding applications, 40-80 dB additional suppression versus single-stage

The design tradeoff involves balancing rated current against inductance and capacitance values. Higher rated current requires thicker wire, reducing the number of turns possible in a given core size and consequently reducing inductance. This inductance reduction can be partially compensated by increasing Y capacitance (within leakage current limits) to maintain common-mode attenuation.

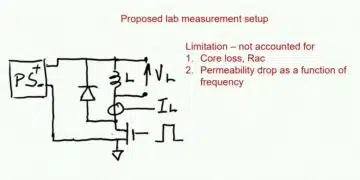
9.2 Measurement and Characterization

Historical practice measured filter attenuation at 50Ω source and load impedance due to network analyzer limitations. Modern characterization employs S-parameter measurements with variable impedance transformation, enabling accurate prediction of filter performance under actual application impedances.

Online tools like REDEXPERT allow engineers to enter actual source and load impedances, calculating expected filter attenuation based on measured S-parameters. This approach dramatically improves design accuracy compared to assuming 50Ω impedances that rarely match real applications.

9.3 Environmental Effects: Temperature and Potting

Core material temperature coefficients significantly affect filter performance across operating temperature ranges. Manganese-zinc ferrite exhibits moderate temperature sensitivity with Curie temperatures of 140-180°C, showing impedance variations of ±20-30% from -40°C to +125°C.

Nanocrystalline materials demonstrate exceptional temperature stability, maintaining nearly constant impedance from -40°C to +180°C with Curie temperatures exceeding 600°C. This stability proves critical for automotive and industrial applications experiencing wide temperature excursions.

Potting compounds encapsulating filter assemblies can mechanically stress ferrite cores during thermal cycling. Low-quality ferrites may exhibit core fracture or significant permeability changes under mechanical stress, degrading filter performance or causing complete failure. Specifying high-quality core materials with robust mechanical properties prevents these failures.

10. Conclusion

Effective EMC filter design transcends simple component selection, requiring systematic understanding of noise mechanisms, frequency-dependent component behavior, and practical implementation considerations. Key principles for successful filter implementation include:

1. Characterize the interference: Identify whether common-mode or differential-mode noise dominates, and determine the frequency range requiring attenuation
2. Select components by frequency response: Inductance values alone provide insufficient information; impedance-versus-frequency curves reveal actual performance
3. Consider parasitic effects: Real components exhibit capacitances, resistances, and layout-dependent inductances that fundamentally alter filter behavior above 1 MHz
4. Optimize placement: Position filters at enclosure entry points, separate input/output wiring, and minimize trace inductances to bypass capacitors
5. Validate through simulation and measurement: Use circuit simulation with parasitic-inclusive models, then verify performance with network analyzer measurements under actual impedance conditions

Modern EMC filter design tools, including S-parameter-based characterization and impedance-variable simulation platforms, enable engineers to achieve first-pass design success. Combined with structured design methodology and awareness of common failure modes, these tools reduce development time while producing optimized, cost-effective filtering solutions.

As switching frequencies continue to increase and EMC regulations become more stringent, disciplined filter design methodology becomes not merely advantageous but essential for product success. The investment in proper component selection, layout optimization, and validation yields substantial returns through reduced certification time, lower production costs, and enhanced product reliability.

FAQ: EMC Filters – From Component to Desig