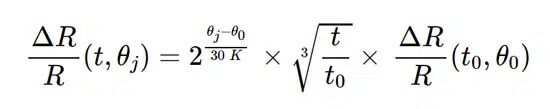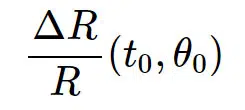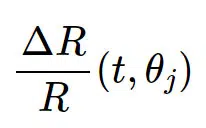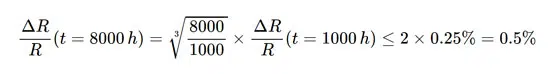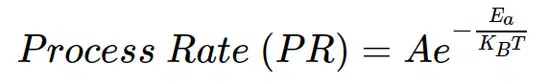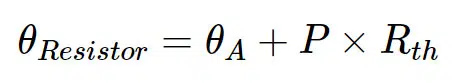Learn about the aging behavior of resistors using temperature calculations and the Arrhenius equation to understand resistor drift and resistors stability in article written by Dr. Steve Arar and published by All About Circuits.
Aging Prediction—Resistor Drift Due to Aging
To begin with, let’s remember that the value of a resistor changes with time. In many circuits, only a gross level of precision is required and the resistor aging might not be a serious issue. However, certain precision applications require resistors with a long-term drift as low as a few parts per million over the specified lifetime.
Therefore, it is important to develop aging prediction models with sufficient accuracy to ensure that the employed precision resistors maintain the specified precision over the entire lifetime of the system. One company, Vishay, suggests using the following equation (Equation 1) to calculate the long-term variation of a thin-film resistor:
where
- Is the reference drift of the resistor at the reference time t0t0 and temperature θ0θ0.
- Is the drift value after the desired operating time of the resistor, t, at temperature θjθj.
Equation 1 shows that raising the resistor’s operating temperature by 30 °K increases its long-term drift by a factor of 2. Additionally, the drift increases with the cube root of the operation time. For example, if the 1000-hour drift of the resistor at 125 °C is less than 0.25%, the resistor drifts after 8000 hours of operation at the same temperature (θj=θ0) is estimated by:
Arrhenius Equation for Resistor Aging Prediction
In Equation 1, the term that takes the temperature dependence into account is derived from the Arrhenius rate law which is also repeated below as Equation 2:
This equation specifies how the speed of a reaction changes with temperature in Kelvin (T). According to Vishay, the aging process of both thin-film and foil resistors obeys the Arrhenius equation.
Figure 1 shows the aging data of identical foil resistors at different temperatures.
In this figure, the natural logarithm of the standard deviation of the resistors’ drift distribution (Ln(DSD)) is plotted against 1000/T.
Note that a straight line can be fit to these data points. This is consistent with the Arrhenius equation, which can be expressed as:
This equation shows that the plot of Ln(PR) versus 1/T is a straight line when a reaction obeys the Arrhenius equation.
Since this relationship holds true for the data points in Figure 1, we can conclude that the aging process of these resistors obeys the Arrhenius law.
Estimate Resistor Temperature – Improving Long-term Resistor Stability
Based on Equation 1, keeping the resistor at a lower temperature can reduce its drift with time. The remaining question is, how can we keep the resistor cooler?
The θ terms in Equation 1 refer to the resistor temperature rather than the ambient temperature. The resistor temperature (θ Resistor) can be estimated by the following equation:
Where:
- θA is the ambient temperature
- Rth is the thermal resistance of the resistor
- P is the power dissipated in the resistor
This equation shows that, in addition to the ambient temperature, the heat dissipated in the resistor and the thermal resistance value can affect the resistor temperature.
For the resistor to run cooler, we can limit the power dissipated in the resistor if possible. Besides, changing the characteristics of the PC board, such as the trace density and the number of the power/ground planes, can change the value of the effective thermal resistance of the system. This change is because the PC board acts as a heatsink soldered to the resistor. A more efficient heatsink or use of SMD thermal conductors can improve heat transfer and keep the circuit components, including the precision resistors, cooler.
Adjusting different design parameters, we can attempt to keep the resistor temperature below a typical maximum value of 85 °C to achieve improved long-term stability.
It is also worth mentioning that operating a resistor at power levels higher than the nominal value can lead to a long-term drift larger than that predicted by the Arrhenius-based equations. Above the rated power, some hot spots can appear in parts of the resistive material where the aging process is accelerated. This can lead to a drift value larger than that predicted by the average temperature of the resistor.
