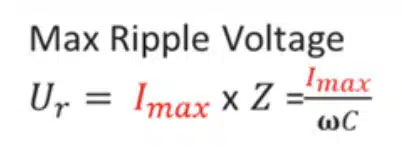Ceramic Capacitors in SMPS Circuits

This technical blog article written by Kevin Cho, KYOCERA-AVX Components Corporation, explains the key parameters for designing ceramic capacitors in SMPS Circuits.

Capacitors are ubiquitous and indispensable components of electronic circuits used for a plethora of uses. For engineers looking to design multilayer ceramic capacitors (MLCCs) in switch-mode power supplies (SMPS) such as Buck and Boost converters, some essential parameters to be considered include the ripple current capability, ripple voltage, and power dissipation.

Using the KYOCERA AVX SpiCalci10 model simulation tool for SMPS capacitors, this whitepaper will outline various MLCC characteristics, AC current capability, and other considerations for circuit design.

Capacitors are critical elements in analog and digital electronic circuits utilized in many applications, including energy storage, coupling and decoupling, electrical noise suppression, bypassing, and more. Different applications have different performance requirements for capacitors with specific characteristics. The size and its materials of construction can be altered to enhance its properties, including:

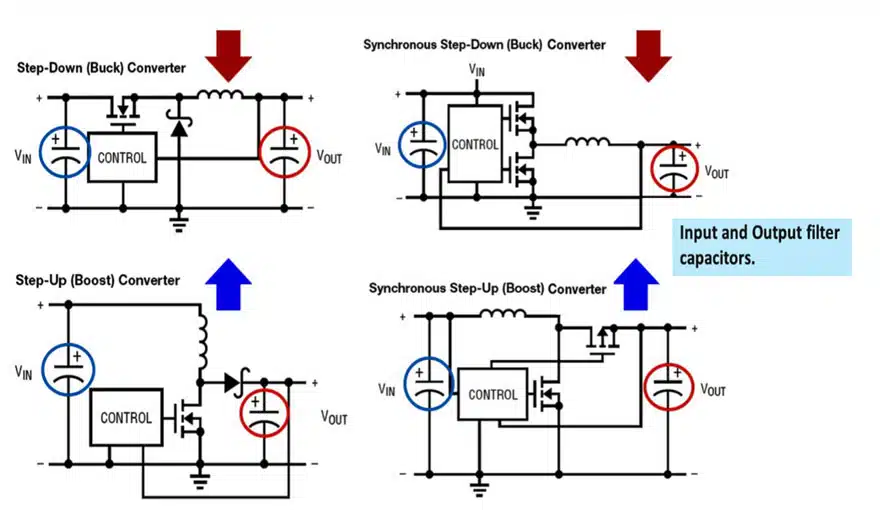
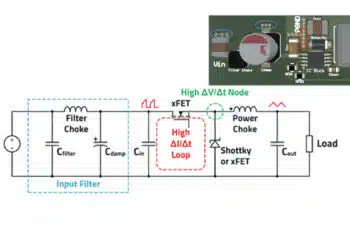
DC-DC Power Conversion in Switched Mode Power Supplies

Figure 1 shows how capacitors are used in voltage regulators:

MLCC Ceramic Capacitors

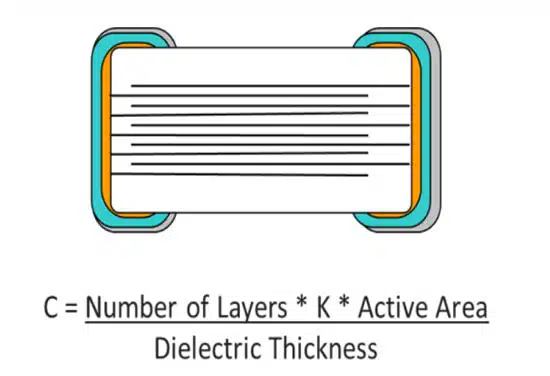
Multilayer ceramic capacitors, also known as MLCCs, are the capacitors of choice in applications requiring small capacitances and are constructed using alternating layers of ceramic and metal. MLCCs are suitable for modern high-frequency applications due to their ultra-low equivalent series resistance (ESR). MLCCs can be broadly classified into two types:

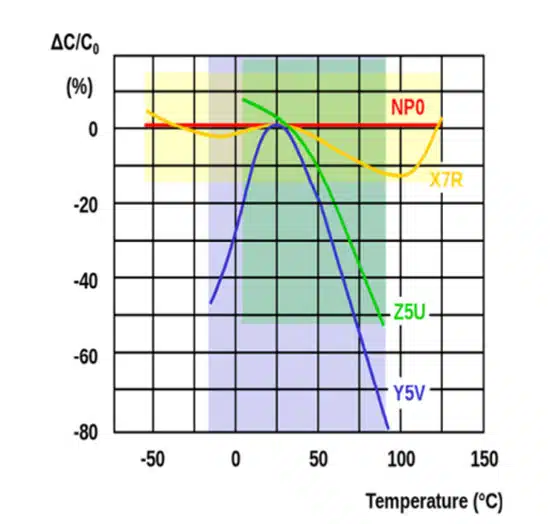
• Class 1: NPO/COG materials (Temperature compensation MLCC)
• Class 2: X7R, X5R, X7S, X6S,Y5V materials (High dielectric constant MLCC)

The main difference between the two is that the capacitance of Class 2 varies with changes in the measurement voltage and temperature, while there is no capacitance variation in Class 1. Figures 2-4 and Table 1 show some of the most important characteristics of MLCCs:

Integrating Capacitors into Electronic Circuits: Series vs. Parallel

MLCCs can be integrated into electronic circuits in two ways: series and parallel connections. Figures 5, 6, and 7 show how to achieve this.

Spice Simulation Software

KYOCERA AVX offers the SpiCALCI 10 (the latest version of its SpiCALCI software), which is an engineering tool that simulates performance characteristics and parameters for its advanced switch-mode power supply (SMPS) multilayer ceramic capacitors (MLCCs).

KYOCERA AVX created this tool to help electrical design engineers select a part that will best satisfy their application criteria. KYOCERA AVX’s SpiCalci10 software allows electrical
design engineers to predict critical parameters, such as self-resonant frequency, ESR, ESL, and phase angle, for a given ambient temperature, temperature rise, and operational frequency. Moreover, designers can adjust the variables numerically, via a button slide, to model important capacitor characteristics, such as ripple current, ripple voltage, and internal temperature.

The software also helps to generate interactive graphs for further analysis of ESR and impedance vs. frequency, temperature rise vs. current, maximum current vs. frequency, maximum ripple voltage vs. frequency, phase angle vs. frequency, and capacitance changes with DC bias. The numerical data can be imported to SPICE simulation software, and the graphs can be saved and printed for presentation or sharing.

Key parameters for designing circuits with MLCCs:

• Allowable ripple current and ripple voltage
• ESR compared to other passive components
• Temperature rise
• Thermal resistance

Maximum Allowable AC Ripple Current: In most electronic devices, the DC current signal applied to a circuit has an AC portion. This AC portion is referred to as the ripple current. The AC ripple current causes power dissipation and heating in capacitors. The power dissipated by a capacitor is a function of the ripple current and its equivalent series resistance (ESR). Heating in ceramic capacitors causes thermal gradients, which could result in degradation and cracking. Thus, ripple current capability is one of the key parameters to consider when selecting a capacitor for a specific application.

Heat Generation Characteristics of MLCCs: When ripple current (AC) flows through a capacitor, the resistor element generates heat, and the temperature rises. However, since the
MLCC offers an extremely small equivalent series resistance (ESR), the heat rise is minimal, and its ripple resistance capability is excellent. Many manufacturers specify the surface temperature of the component to be below 20 °C. Figure 8 shows a mathematical formula for calculating the maximum allowable ripple current of MLCCs:

Ripple Voltage (RMS) For Ceramic Capacitors: A simple formula for calculating the maximum ripple voltage of a ceramic capacitor is:

where:

• Ur = maximum ripple voltage (rms)
• Imax = maximum allowable rms value of ripple current
• Z = impedance
• ω = 2πf
• C = capacitance

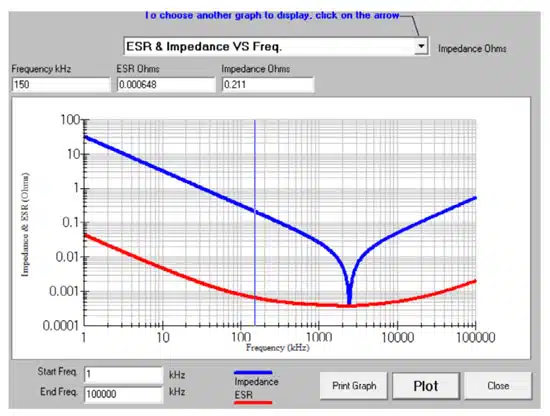
ESR Constitution: Because practical capacitors are non-ideal components, they offer some level of resistance within their constitution. When integrated in series in electronic circuits, the equivalent series resistance (ESR) is an essential parameter. Alongside the capacitance, the ESR defines a time constant for charging or discharging the capacitor and how quickly it reacts to variations in voltage, current, and ripple. Figure 11 shows the ESR constitution of a ceramic capacitor.

where:

• tan δ = dissipation factor of the capacitor
• tan δ0 = dissipation factor of the dielectric
• C = capacitance
• Rs = series resistance
• ESR = equivalent series resistance

Maximum Temperature Rise: As previously mentioned, when ripple current passes through a capacitor, power is dissipated in the form of heat, resulting in temperature rise (self-heating). Other factors include dielectric losses and the temperature of the surroundings (ambient temperature).

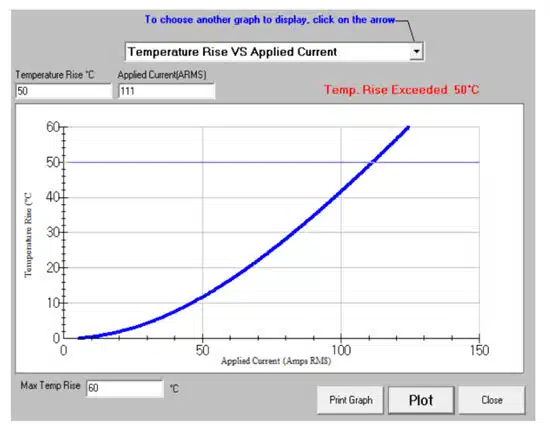
All of these factors compound to affect the temperature of an MLCC. Since MLCCs are dependent on temperature and not current, variations in the temperature will determine the maximum ripple current. The maximum temperature rise of ceramic capacitors is usually limited to 50°C to prevent damage to the component (cracking) due to thermal gradients.

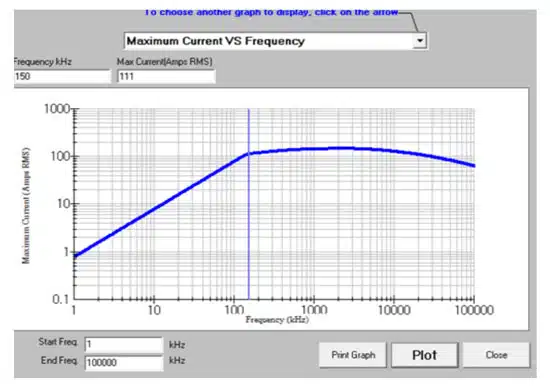
For example, take a X7R MLCC with a temperature range from (-55°C to 125°C). When the circuit is operating at +25°C, the MLCC can handle enough current until the part has heated up to 125°C.

However, when the same circuit is at 100°C, the ripple current would be less as there is a lower temperature differential. The KYOCERA AVX SpiCalci10 simulation below shows temperature rise vs. applied current with the following parameters:

• Imax = 111A(rms)
• Irms = 66.3A(rms)
• ΔTmax = 50°C
• ΔT = 20°C

Key Parameters for Designing Ceramic Capacitors in SMPS Circuits

Ripple Voltage (RMS) for Ceramic Capacitors

The maximum ripple current voltage in the application shall not exceed the maximum ratings of the capacitor. KYOCERA AVX SpiCalCi10 simulation of maximum ripple voltage vs. frequency as shown in Figure 10. can be used to assess capability of the selected part versus the real application requirements at desired frequency range.

Thermal Resistance

The thermal resistance (Rth) between a capacitor and the environment is a function of the airflow over the capacitor, the surface area of the capacitor, and any heat sinking of the capacitor. To specify the most conservative (lowest) values of ripple current capability, the thermal resistance of the MLCC is measured under still air with no heat sinking at 25°C ambient temperature.

Rth will be different for each case size as it depends on both the internal construction of the capacitor (pellet size and thermal paths) and the external surface area. Recall that thermal gradients caused by the heat generated by ripple currents can crack the ceramic chip. Electrode plates act as heat sinks, and capacitors with a high number of plates release heat from ceramic blocks more easily than components of the same size but with fewer plates.

Conclusion

Internal heating within ceramic capacitors affects the performance of many electronic circuits. In these capacitors, the maximum ripple current is determined by the temperature characteristics of the component.

Exceeding the ripple current rating of a ceramic capacitor can significantly affect its performance. The coefficients of thermal resistance for ceramic capacitors of a given chip size vary due to differences in the number of electrode plates.

Heating in ceramic capacitors causes thermal gradients that could result in physical damage such as cracking. The maximum temperature rise in ceramic capacitors is usually limited to 50°C to prevent cracking.