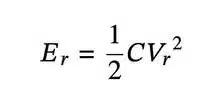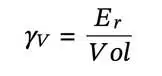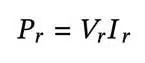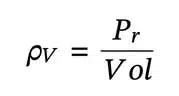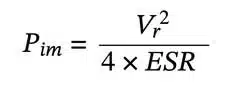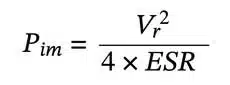This article describes capacitor energy content, what energy can be stored and delivered by the capacitor and what forces present inside a capacitor. It also describe basic concepts of capacitor energy density and power density and their impact on capacitor performance.
Energy density and power density are two crucial yet distinct metrics in the field of energy storage. Understanding the differences between these two metrics is essential for designing efficient energy storage solutions.
Key Takeaways
- Capacitor energy density measures how much energy a capacitor can store per unit mass or volume, crucial for applications where space is limited.
- Power density indicates how quickly a capacitor can deliver energy, impacting performance in fast-response applications like lasers or camera flashes.
- High energy density benefits long-term storage, while high power density allows for rapid energy transfer, necessitating a design balance.
- Capacitance and voltage determine the energy stored in capacitors, while equivalent series resistance (ESR) affects their power density.
- Understanding the forces in magnetic and electrostatic fields is vital for analyzing capacitor behavior under high voltage conditions.
Comparing Energy Density and Power Density
Energy density describes the amount of energy stored in a mass (Wh/kg or J/kg) or volume (Wh/L). High energy density implies the system can store a lot of energy in space- and weight-constrained spaces. This is particularly useful in applications like mobile devices and electric vehicles where board space is a luxury and long-term energy storage is critical for operational efficiency.
While frequently mentioned together in energy storage discussions, energy density and power density represent distinct performance characteristics. Power density describes how quickly energy can be delivered or absorbed into a system in W/kg or W/m3. High power density tells us a system can release or accept energy at a fast pace. This characteristic best serves applications that require quick bursts of energy like camera flashes or industrial lasers.
In short, energy density focuses on storage capacity while power density measures the rate of energy transfer, and systems designers are expected to balance the two. For example, batteries with high energy density may not be able to deliver energy as quickly as supercapacitors, which are known for their high power density.
Capacitor Energy Content and Power Density Math
The energy stored in a capacitor is expressed using:
where
- C is capacitance
- Vr is the voltage rating of the capacitor.
To find the volumetric energy density of a capacitor, divide Er by volume:
The power rating of a capacitor can be estimated from the rated voltage and current as :
Power density is Pr divided by volume:
Alternatively, another approach to determining power density is to examine the impedance-matched condition, where the load matches the source impedance (i.e., the capacitor’s equivalent series resistance (ESR)). Under these conditions, we find:
Then, power density is calculated as:
This method reveals that capacitors with high power density require a low ESR to maximize the rate of energy transfer. As a result, innovation in capacitor design focuses on optimizing capacitance and voltage within a compact volume while minimizing internal losses from ESR.
Electromagnetic Fields Force action
Parallel current carrying conductors are surrounded by magnetic fields exerting forces on each other. If currents flow in the same direction the fields (and the conductors) attract each other. If the current flows in opposite directions they are repelling each other.
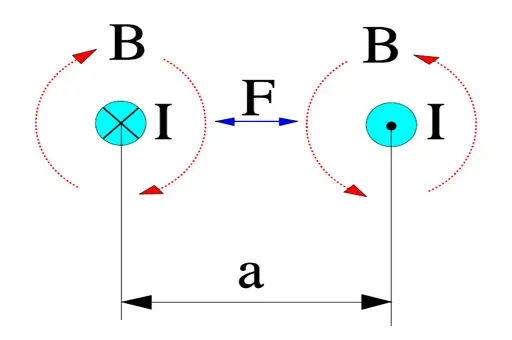
If
- the conductor length l is expressed in m,
- the current I is expressed in A and
- the distance a is expressed in m,
the force per meter between the conductors will be
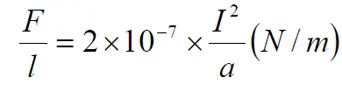
………………………[2]
According to the basic charge formula Q = C x V (As). If this expression is derived we obtain dQ/dt = I = C x dV/dt (A). Pulse loads are not unusual, especially in conditions with high voltage gradients, and thus high charging currents also occur which might cause appreciable magnetic fields between close lead patterns, for example.
Force action in electrostatic fields
Capacitors are typical examples of applications where electrostatic fields are applied. These fields can generate significant mechanical forces. If we know the electrode distance d (m) it’s easy to determine the electric field strength E (V/m). Then we can outline the force per unit area, i.e. the pressure that the electrodes exert on the dielectric.
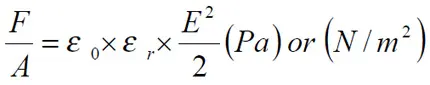
……………………………….. [3]
Example. Suppose we have an oil impregnated paper capacitor with r = 5 and the dielectric = 15 m (0.6 mils) which is loaded with 250VAC. Then the instantaneous maximum pressure will be
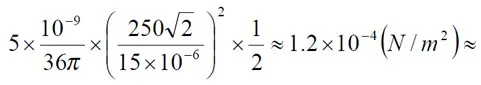
0.1 kp/cm2 !
If we instead calculate on a 35 V solid tantalum capacitor with a typical and approximate dielectric thickness of 0.2 mm (0.008 mils) the formula gives at 30 V DC a pressure of
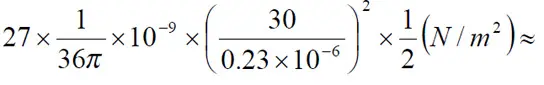
2 N/mm2 !
It is difficult to determine how much the dielectric is influenced by such forces, especially when the electrodes have such complex configurations. Electrostatic action of such forces here is of vital importance.
Electrostatic Force Potential Impact
We learned in the article about the energy stored in the capacitor, but what is also important and demonstrated is that there is enormous mechanical pressure between the electrodes once voltage is applied.
This can be considered in failure analyses if we have a solid, sharp impurity within the capacitor dielectric – it may degrade the insulator not only by inducing electrical conductivity/increasing leakage current, but also causing a mechanical damage to the dielectric due to the high electrostatic pressure between the electrodes. Hard and sharp micro-crystals in amorphous dielectric could be an example of such defects.
FAQ: Energy Density, Power Density and Capacitor Energy Content
Energy density is the amount of energy stored per unit mass or volume of a capacitor. It is typically measured in Wh/kg or Wh/L, reflecting how much energy can be packed into a limited space. High energy density is essential for efficient storage in mobile and compact devices.
Power density measures how quickly a capacitor can deliver or absorb energy, expressed as W/kg or W/m³. High power density means the component can respond rapidly to energy demands, useful for applications requiring fast energy pulses like camera flashes or lasers.
Energy density focuses on total storage capacity, while power density emphasizes the rate of energy transfer. Capacitors may have high power density for fast delivery, whereas batteries typically have higher energy density for longer storage.
Equivalent Series Resistance (ESR) impacts power density. Low ESR allows capacitors to transfer energy faster, making it a key design factor for high-performance capacitors.
How to Calculate Capacitor Energy Density and Power Density
- Calculate Stored Energy
Use the formula E = ½ × C × V², where C is capacitance and V is the rated voltage.
- Determine Volumetric Energy Density
Divide the stored energy (E) by the capacitor’s volume to obtain energy density in Wh/L or J/m³.
- Estimate Power Rating
Calculate power using the rated voltage and current. Then divide by volume to find power density.
- Consider ESR Effects
Under impedance-matched conditions, low ESR maximizes power density. Always account for ESR when designing capacitors.