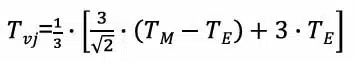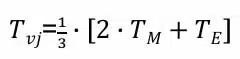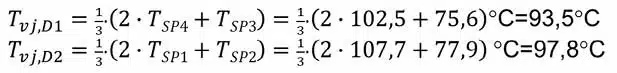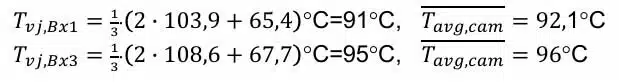This article written by Dr.-Ing. Martin Schulz, Global Principal, Application Engineering, Littelfuse, provides insight into how to determine packaging chip temperature.
The most prominent factor for determining the service life of a power-electronic system is the temperature development at the passive or semiconductor components itself. For this reason, it is very important to determine the chip temperature as accurately as possible.
The determination of a power chip device’s temperature often is not a trivial task. This is partially because strictly speaking there is no such thing as “the chip temperature”. All specifications in data sheets and in calculations on service life refer to a mathematical construct of a virtual chip temperature or virtual junction temperature Tvj.
The so-called in-situ measurement is the method of choice to measure the chip temperature in the laboratory. Here, the chip to be measured is first heated to precisely defined temperatures using a calibrated heating plate. A small measuring current is then injected, and the resulting forward voltage is measured. There is a linear relationship between the forward voltage and the temperature of the chip, provided that a constant and precisely known current is flowing.
The current must be chosen small enough, so that it does not itself contribute to the heating of the measured passive or semiconductor component. At the same time, it but must be sufficiently large to generate a measurable voltage. Values around 1% of the nominal current of the semiconductor to be tested have proven to be reasonable.
In turn, the chip-temperature can be determined from the correlation, which is unique and reversible, if the previously used current is used and the voltage on the component is known. The result of this laboratory measurement is based on a constant chip temperature and, due to the external heating, there is a homogeneous temperature distribution in the chip. This special case, which does not reflect the conditions in the real application, provides “the chip temperature” or the “junction temperature” Tj.
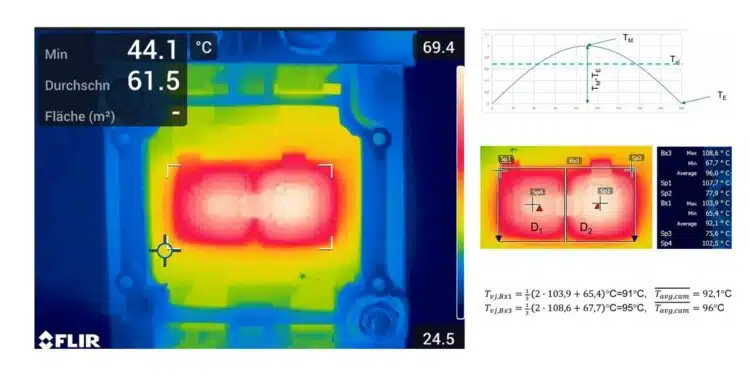
In the real application, however, there is a temperature gradient across the chip’s surface; the chip is hotter in the center than it is at the edges, especially at the corners. The reason for this is that more heat can be transferred to the surrounding assembly and connection technology at the edges and corners than in the center of the chip. The effect can be clearly seen in measurements such as those displayed in Figure 1, which are taken using an infrared imaging camera (IR).
Alternatively, a sensor placed on the chip is often used, for example a type K thermocouple. Although the sensor then provides a temperature value, this does not necessarily represent the value required for characterization and service life determination. One advantage of this measurement is that it is possible to measure during operation at high voltage and high current, provided the measurement equipment meets the requirements for the protection
of equipment and personnel. This is important as the sensor is in galvanic contact with the chip and therefore carries a potentially lethal voltage.
The temperature sensor is often placed in the center of the chip, so that it at least reliably delivers the maximum value. If the thermal relationships are known precisely enough, conclusions can also be drawn from the maximum value to the average value. The virtual chip temperature Tvj, which represents an average value of the temperature over the entire chip surface, is always of interest when considering the service life and thermal design. If it can be implemented, the in-situ measurement also precisely provides this value in the real setup, as only one voltage at one current needs to be measured. Averaging is an inherent part of this measurement setup. The measured voltage represents the chip temperature as if it were homogeneously distributed.
Reliability tests at component manufacturers are also monitored using the in-situ method. Here the approach is close to the application as the chip is actively heated. The information on load cycling resistance based on this method already includes the fact that the maximum temperature value on the chip is higher than the temperature specified. This approach can therefore be considered conservative and is ideally suited to characterization measurements and quality assurance processes.
Another way to calculate the mean value is by evaluating IR images. This method also allows the observation of semiconductors in real operation and provides precise and application-related information. For evaluation, the software belonging to the IR camera usually allows an area of interest to be defined and the correlating mean value within it to be determined. This procedure is used in Figure 1; the area under consideration comprises two diodes connected
in parallel. The disadvantage of this method is that the observed semiconductors must not be potted. Potting compounds, even if they are optically transparent, block the emitted infrared radiation, making this way of measurement impossible. Consequently, such setups cannot be operated with high voltages because the lack of insulation can lead to arcing and malfunction or even destruction.
A frequently used alternative evaluation consists of determining the temperature TM in the center and the temperature TE in one corner of the chip and performing a 2-to-1 weighting. The virtual chip temperature then results in Tvj=1/3·(2·TM+TE). This is possible both from the IR image and using two correctly positioned temperature sensors. It is no coincidence that even this seemingly simple method delivers accurate values. The precision can be explained by the thermal conditions along the chip diagonals.
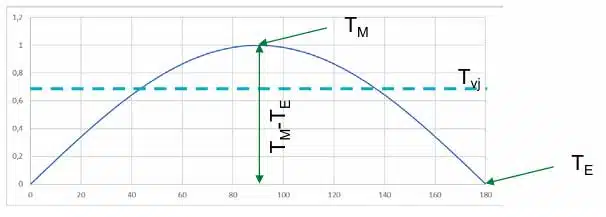
From one corner to the diagonally opposite corner, the temperature across the chip develops along a dome-shaped curve. A good approximation of this shape is either a parabola or a sinusoidal curve. Due to the simple relationships, the sinusoidal curve is the preferred one here. The mean temperature results from the effective value of the sine curve and the offset. Figure 2 depicts the curve that can be assumed in this case.
The required mean value corresponds to the RMS value, which is calculated from the amplitude (TM-TE) and the offset TE as:
In another notation, the equation can be rewritten as:
with the approximation 3/SQRT(2) ~ 2 the result is:
A comparison of the three methods for averaging – in-situ, area average and 2/3 approximation – results in slightly different numerical values. If the tolerances of the respective measuring techniques are considered, it turns out that the values usually only deviate slightly from each other in the range of ±1K.
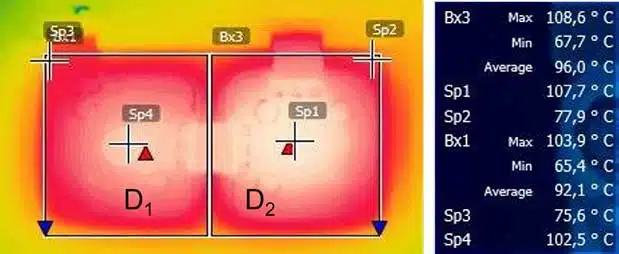
Figure 3 gives an insight into the data obtained using an IR camera from a measurement on two diodes connected in parallel within a semiconductor module.
The measuring points Sp1 and Sp4 in the middle of the diodes and Sp2 and Sp3 at their corners, which are clearly visible in Figure 3, are used for the 1/2 weighting. These measuring points were placed by hand, so there are also tolerances here. Based on the local values determined, the virtual chip temperatures for the diodes are:
The evaluation of the mean value over the entered areas Bx1 and Bx3 and the automatically displayed maxima and minima provide:
As a result, this means a temperature of 92.25±1.25°C for diode D1 and a temperature of 96.4±1.4°C for diode D2. Although in both cases neither the true maximum nor the true minimum was met, the deviation of values finally determined is negligible.
What is the practical use and gain for developers?
Determining the chip-temperature is crucial to support simulation results that are often starting points when predicting lifetime of a system under development. Chip temperature measurement during operation tends to be challenging. Thus, the recurring request is, to get a customized power device with a thermal sensor attached to the chip.
Instead – and if chip-sizes allow to do so – placing two sensors will get a very accurate result of the chip-temperature, even under operating conditions. The very similar results all methods lead to also substantiate how robust the 1/2 averaging is when there is a setup with two thermocouples.