This article introduces some key electrical resistor parameters such as resistivity, thermal resistance and TCR temperature coefficient.
Resistivity (ρ)
The resistivity, ρ, is a material constant. The higher the resistivity in the resistor material, the higher its resistance. The connection can be described as
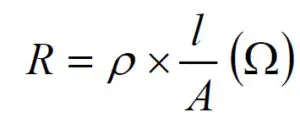
Here
R = resistance
l = conductor length
A = conductor area.
Depending on what units we express l and A in we get different units of ρ. A common way is by expressing l in m(eter) and A in mm2 , ρ then gets the unit Ω.mm2/m. If we instead choose l in m and A in m2, the unit for r will be Ω.mm2/m, which usually is transformed to Ωm. That unit often is used for non-metallic materials. If we know the value of ρ expressed in Ω.mm2/m, that value has to be multiplied by the factor 10-6 to give the value in Ωm. Thus, 10-6 x Ω.mm2/m = 1 Ωm.
Sheet Resistivity (Ω/square)
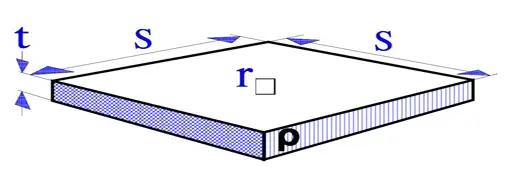
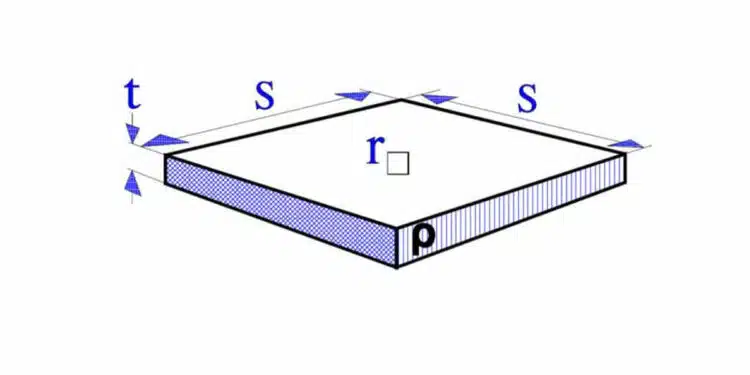
The sheet resistivity is a measure of the resistance per surface unit of resistive films. A square surface element as shown in Figure 1. gets according to the formula [1] the resistance:
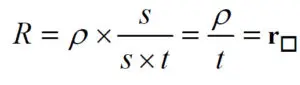
Thus, the resistance per square unit, r(sq), is independent of the surface size. It is the film thickness and its intrinsic resistivity that determine r(sq) (expressed in Ω/square).
Surface Temperature and HOT SPOT
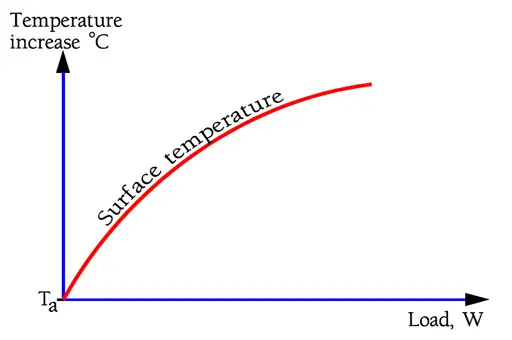
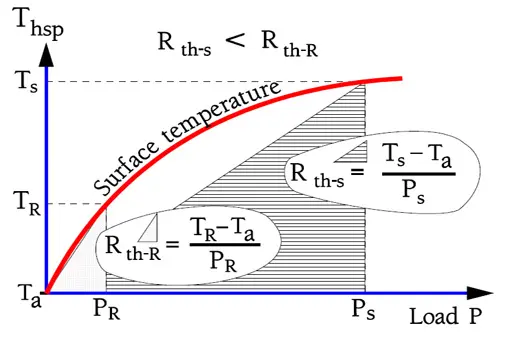
The surface temperature rise of the resistor body depends on the load as shown in principle in Figure R2. As temperature rises, conduction, radiation and convection (air-cooling) from the resistor body increases which causes the temperature curve to level off.
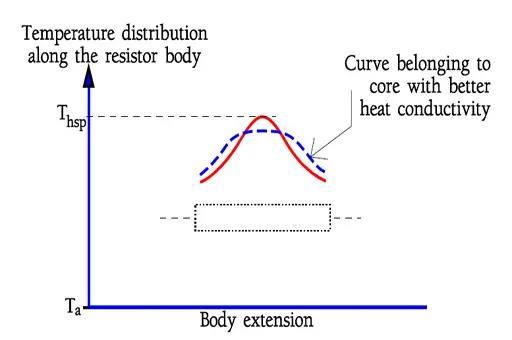
Figure 3. shows the temperature distribution along a resistor body. Thermal dissipation to the leads or SMD terminals decreases the temperature at the ends. In the middle of the body we register a temperature maximum, the so called Hot Spot temperature. This temperature determines both the resistor stability and life.
It is important that spiraling or wire winding be spread uniformly over the whole free resistor length. Otherwise we get an intensified Hot Spot effect that endangers life and stability.
It is not only for the resistor itself the Hot Spot is of vital importance. Heat radiation may have an effect on adjacent components and circuit boards. Thus, see that there is a satisfactory distance to the resistor body from heat-sensitive adjacent components.
Thermal Time Constant, τw
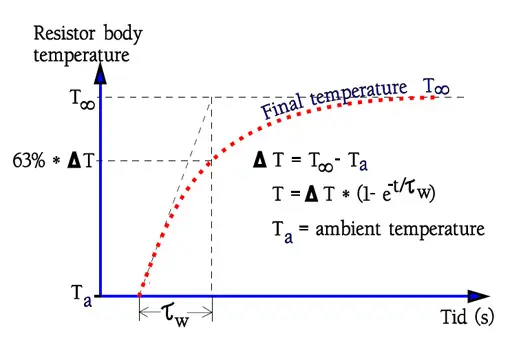
The thermal time constant, τw, is defined as the warm-up time for the resistor surface to attain 63% or theoretically (1-1/e) of the final temperature after applied load is increased in steps, usually PR (Figure 4). Of course, the time constant is strongly dependent on the resistor body size. It will be quicker to heat up a small body than a big one. Table 1 states standard values for some DIN classified sizes.
| DIN size | 0204 | 0207 | 0414 |
| Thermal time constant, τw (s) | 2 | 5 | 20 |
| Thermal resistance, Rth (K/W) | 400 | 250 | 170 |
Thermal Resistance, Rth
The thermal resistance, Rth, is expressed in K/W. It describes the temperature increase of a resistor body under applied load. Since radiation causes the temperature curve to turn downwards at increasing load data about Rth concerns normalized mounting and a load of PR. (See DIN 44 050). As shown in Figure 5. an power overload reduces the Rth.
In Equation [3] below the connection between Rth and current temperatures is described. Rth is expressed in K/W but due to the fact that the equation deals with the difference between two temperatures it doesn’t matter if we use °C or K for both values. The differences will be equally large. K2-K1 = [(°C2+273) – (°C1+273)] = °C2-°C1.
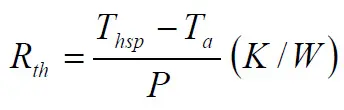
Thsp = Hot Spot temp. in K or °C
Ta = ambient temp. in K or °C.
P = applied load, W.
In Table 1. there are some examples of the thermal resistance for standard DIN sizes.
Temperature Coefficient of Resistance, TCR
The temperature coefficient of resistance, TCR, is expressed in ppm/°C.
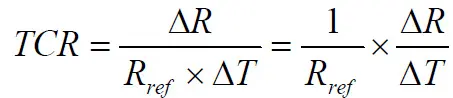
For clarification reasons TC is often written TCR, i.e., Temperature Coefficient of Resistance.
Specification limits and actual changes may look like the ones in following figure where a family of components are shown.
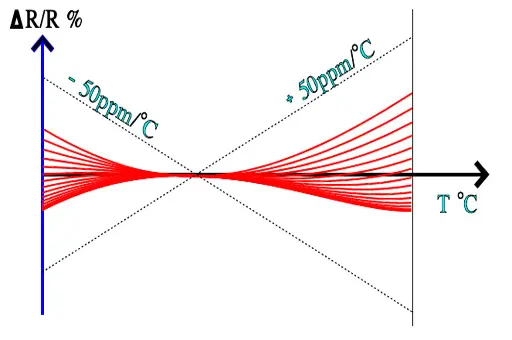
Temperature coefficient of resistance is of key importance especially at high precision resistors. In-depth article with more insights can be studied here:
Understanding High-Precision Resistor Temperature Coefficient of Resistance
Temperature Rise and Heating of Resistor
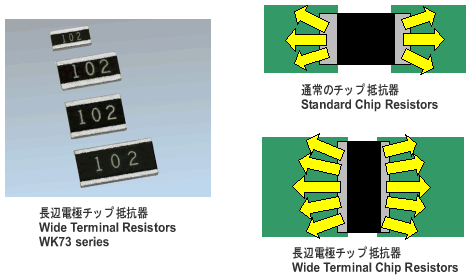
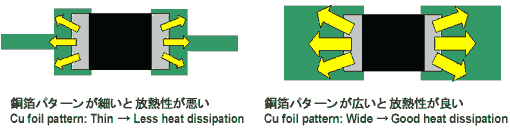
Resistor is an element that converts electric energy into heat energy. It always generates heat when the electric power is consumed and the temperature rises according to the consumed power. To control the temperature rise of a resistor, the generated heat needs to be dissipated efficiently. For chip resistors, the most of the generated heat conducted from the electrode to Cu foil pattern on the PCB, and finally dissipated to the air or chassis. As the image below, expanding the pad pattern of the resistor or expanding Cu foil pattern where the resistor is connected, will lead to good heat radiation and control the temperature rise.
Temperature rise of the resistor is also controlled by improving thermal conductivity of PCB; by thick Cu foil pattern, forming solid pattern on the back side of PCB or solid pattern inside the layer if it is a multilayer substrate. Wide terminal type flat chip resistors (reversed geometry) have excellent heat radiation characteristic and perform under high power. Examples of the wide terminal flat chip resistors are shown below. Forming the electrodes on long sides of this type of resistor, shortens the distance between the heat generating point and the electrode, enables to conduct much volumes of heat to PCB by large electrodes, which leads to improve heat radiation of resistor. The rated power is much more improved than that of standard resistor in same size.