Understanding Inductors With Gapped Cores

Inductors are fundamental components in electronic circuits, used extensively for their ability to store energy in a magnetic field. The design and selection of inductors can significantly impact the performance of a circuit, especially in power supply and radio-frequency applications. One critical aspect of inductor design is the use of gapped cores, which introduces an air gap into the magnetic path of the inductor’s core. This blog post delves into the nuances of air-core versus magnetic-core inductors, the concept of gapped cores, and the implications of introducing an air gap in inductors.

Air-Core vs. Magnetic-Core Inductors

The primary distinction between air-core and magnetic-core inductors lies in the presence of a magnetic material in the core. Air-core inductors do not contain a ferromagnetic core; instead, they rely on the air itself to form the magnetic circuit. This design is advantageous at high frequencies where core losses in magnetic materials can become significant. On the other hand, magnetic-core inductors use materials like iron or ferrite to concentrate the magnetic field, resulting in higher inductance values for a given size and number of turns.

Gapped Core Inductors: An Overview

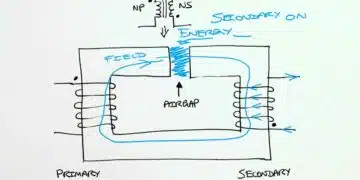
A gapped core inductor incorporates a deliberate air gap in the magnetic core. This gap is introduced to manage the core’s saturation and improve its current-handling capability. By adding an air gap, the inductor’s inductance decreases, but its ability to handle higher currents without saturating increases. The air gap also contributes to stabilizing the inductance against variations in the core material’s permeability, making the inductor’s performance more predictable.

Analyzing the Gapped Core

The introduction of an air gap affects several parameters of an inductor. It reduces the effective permeability of the core, which is a measure of the core’s ability to support the formation of a magnetic field. A lower effective permeability means that the inductor will have a lower inductance value for the same number of turns and core area. However, this also means that the inductor can tolerate a higher current before the core material saturates.

Effective Permeability of Gapped Core

Effective permeability is a critical factor in designing gapped core inductors. It represents the average permeability of the core material and the air gap. The presence of the air gap reduces the effective permeability significantly, as air has a much lower permeability than ferromagnetic materials. This reduction in effective permeability is beneficial in applications where a stable inductance value is crucial, as it makes the inductor less sensitive to changes in the core material’s properties.

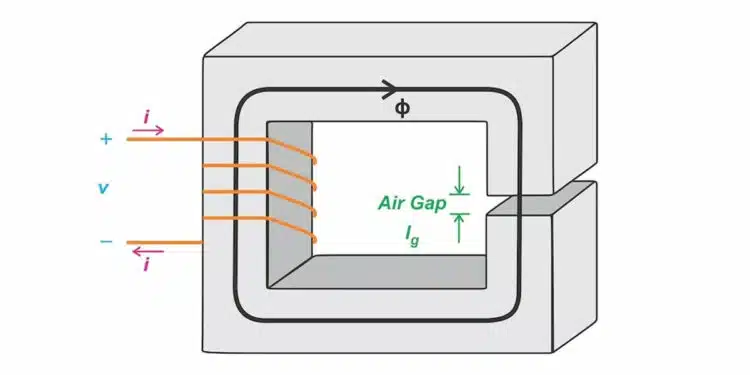
Based on the featured image to see how the air gap influences different inductor parameters. Assume that:

• The core has relative permeability μ_c and mean length l_c.
• The gap has a relative permeability of unity and a length of l_g.
• The cross-sectional areas (A) of the core and the air gap are equal.

If the permeability of the core is much larger than unity (μ_c ≫ 1), a gapped core has an effective relative permeability of:

μ_eff ≈ l_c/l_g

where:

l_c is the mean length of the core

l_g is the gap length.

When l_c = 100l_g, for example, the gapped core has an effective relative permeability of 100. The important takeaway here is that the gap dominates the core behavior as long as μ_c ≫ 1.

Impact of Air Gap on Inductance and Material Permeability

The air gap’s impact on inductance is twofold: it reduces the inductance value and decreases the sensitivity of the inductance to the core material’s permeability. This desensitization is particularly useful in environments with temperature fluctuations or in applications where the inductor is subjected to varying currents, which can otherwise alter the core’s permeability and, consequently, the inductance.

Since the gap lowers the effective relative permeability of the core, it’s no surprise that adding a gap also lowers the inductance of the structure. Another way to reach the same result is by applying the definition of inductance. We know that inductance is defined as:

L = nΦ/i

we find the inductance of the gapped core to be:

L = n²/(Rmc + Rmg)

The air gap increases the total reluctance and decreases the inductance. Despite this apparent decrease, gapped cores offer three important advantages:

• They reduce sensitivity to material permeability.
• They increase the saturation current.
• They increase the stored energy.

Without an air gap, the inductance is directly proportional to the core material permeability, which changes with temperature and is a nonlinear function of the applied magnetic field intensity. This makes it hard to precisely control the inductance.

Now consider a gapped core. Since the reluctance of the air gap is much larger than that of the core material:

L ≈ n²/R_mg = n²/(l_g/μ₀A) = n²μ₀A/l_g

From the above, we can see that a gapped core’s inductance depends mainly on the gap properties (A and l_g). Since the permeability of air (μ₀) is constant, it’s possible to adjust the gap length to build well-controlled inductances that are less sensitive to variations in permeability.

Increasing Saturation Current and Stored Energy

By introducing an air gap, the saturation current of the inductor increases. This is because the air gap requires a higher magnetomotive force (current times the number of turns) to achieve the same flux density in the core as would be needed without the gap. As a result, the inductor can handle higher currents without the core material reaching saturation. Additionally, the air gap allows the inductor to store more energy, which is advantageous in power applications where energy storage is essential.

When a gap is introduced into the core, the effective reluctance increases. A larger current is thus required to saturate the core. Let’s calculate the maximum current that the inductor can handle without reaching saturation.

the B value of a gapped inductor is given by:

B = ni/(R_mc + R_mg)Ac

where A_c is the cross-sectional area of the core. The current at the onset of saturation, therefore, is:

I_sat = B_satA_c*(Rmc+Rmg)/n

where B_sat is the saturation magnetic flux density. The air gap increases the effective reluctance, and hence the saturation current, of the core.

Choosing Gap Length and Number of Turns

Selecting the appropriate gap length and number of turns is a balancing act. A larger gap can increase the inductor’s current-handling capability but at the expense of reduced inductance. Conversely, increasing the number of turns can compensate for the reduced inductance due to the air gap but may result in a physically larger inductor. Engineers must consider these trade-offs in the context of their specific application requirements.

We saw that the air gap increases the saturation current but lowers the inductance. To compensate for the loss of inductance due to the air gap, we can increase the coil’s number of turns (n). This increases the magnetic field generated by the coil, restoring the inductance to the desired value.

Assuming that the gap reluctance is much greater than that of the core:

L ≈ n²/R_mg

and:

B ≈ ni/R_mgA_c

Increasing the value of n causes both the inductance (L) and the magnetic flux density (B) to increase as well. However, L is proportional to n² and B is proportional to n. The inductance therefore grows faster than the flux density when n is increased.

Conclusion: The Advantages of Air Gapped Inductors

Air gapped inductors offer several advantages, including increased saturation current, reduced sensitivity to core material variations, and enhanced energy storage capabilities. These benefits make them suitable for a wide range of applications, from power supplies to RF circuits. Understanding the interplay between the air gap, inductance, and saturation current is crucial for optimizing inductor design for specific applications.

In summary, gapped core inductors are a versatile and robust solution for managing the performance of inductors in various electronic applications. Their ability to maintain stability under different operating conditions makes them an invaluable component in the design of reliable and efficient electronic systems.

All of these advantages are achieved at the expense of a smaller inductance. However, by appropriately choosing the gap length and the number of turns, we can restore the desired inductance while avoiding core saturation. This technique is commonly used to design inductors for power electronics applications.