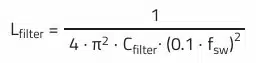This article elaborates on the properties and design of input filters for DC/DC converter applications. The post is based on Würth Elektronik‘s “DC/DC Converter Handbook” which can be ordered from WE website here. Published under permission from Würth Elektronik.
As described in Selection of Capacitors for DC/DC Converters, despite a suitable design of the input capacitor, there is no way around an additional input filter in many applications. Probably the most widely used topology – the buck converter – is particularly affected by this.
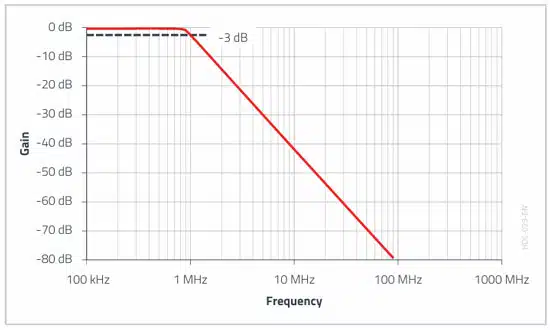
Attenuation values of up to 30 dB are required in practice. This attenuation is easy to realize with a classic 2nd order filter; an “LC” low pass.
The low pass theoretically provides up to 40 dB attenuation per frequency decade. Due to the parasitic inductances in the capacitor and on the PCB, this value is not quite attained in practice. Nevertheless, with a skilled choice of components, 30 dB attenuation is quite an easy value to achieve.
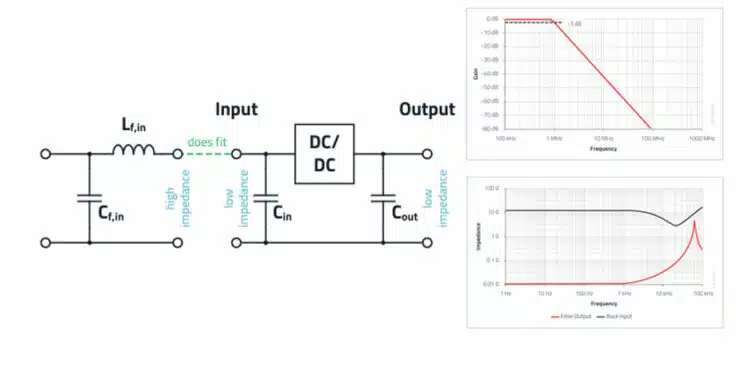
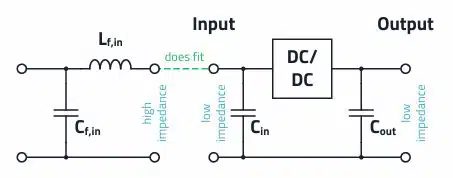
The LC input filter must be configured as in Figure 1., because the input capacitor of the converter represents a low impedance. In contrast, the filter inductor has a high impedance. Together with the filter capacitor, this forms an LC low-pass filter from the viewpoint of the DC/DC converter.
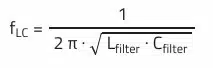
As mentioned in the “Selection of Capacitors for DC/DC Converters” it is useful to orientate the filter design primarily to the converter’s switching frequency. If this frequency is reduced by the filter in the spectrum, e.g., by 30 dB, the next harmonics of this fundamental frequency are naturally reduced in turn. This is easy to show with the help of Thomson’s oscillation equation:
This equation describes the –3 dB point of the filter cut-off frequency. From this point onward, the LC filter theoretically provides 40 dB of attenuation per frequency decade.
If this frequency point is now set to 1/10 of the switching frequency (for example at 1 MHz, this is 100 kHz), then in the ideal case 40 dB filter attenuation is obtained. Sample calculations are given in the following chapters. A good compromise between component size, cost, and the parasitic characteristics of the filter elements for many DC/DC converters results in:
Filter inductor: From 0.47 µH to 22 µH
Filter capacitor: From 1 µF to 100 µF
The inductance values of the filter inductors should be selected as low as possible to obtain a small DC resistance for a given component size, as well as not to compromise the stability of the DC/DC converter. A shielded filter inductor can be beneficial if it is placed very close to the DC/DC converter, as this reduces magnetic interference coupling.
Generally, it is beneficial to freely select the value of the filter capacitor and then use the formula below to determine the inductance value of the filter inductor:
Input stability criteria
If a filter is placed in front of a DC/DC converter, in practice this can lead to undesirable effects under certain circumstances:
• Deeper voltage dip and longer output voltage overshoot of the converter with a load step
• Pronounced oscillation of the voltage at the converter input
The reason for such effects is that the resulting impedance of the LFilter – Cin resonant circuit at the DC/DC converter input is too high. A converter with a filter is considered stable if the output impedance of the filter is significantly lower than the input impedance of the DC/DC converter over a certain frequency range in which the control loop is active.
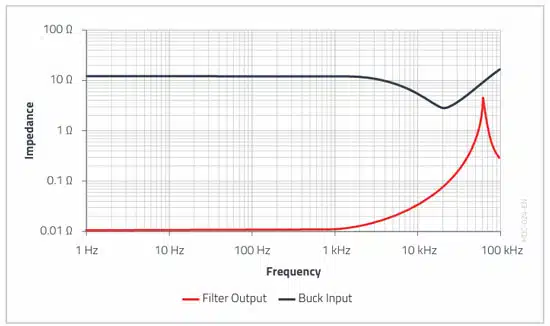
The example in Figure 3. shows that the red curve comes very close to the black curve in a certain frequency range. Here the filter inductance resonates with the input capacitor of the DC/DC converter (not with the filter capacitor, as is often wrongly described!). As these are high Q components in practice, this pronounced impedance rise occurs at the resulting cut-off frequency of Lfilter and Cin.
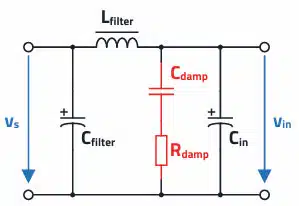
To reduce Q, and thus also the impedance rise of the resulting resonant circuit, it is usual to connect an attenuation capacitor Cdamp (possibly plus an external resistor) in parallel to the input capacitor. This capacitor should have a capacitance at least 3 to 4 times greater than the input capacitor and a dissipation factor as high as possible (e.g., aluminum electrolytic capacitors with high ESR).
In addition to the ESR, a low-inductance external SMT resistor Rdamp should also be used. In both cases, the maximum possible power loss of the components must be considered. In the capacitor branch, a purely ohmic loss resistance is required in any case to reduce the quality factor. The specification of 3 to 4 times the capacitance is justified by the fact that the reactance of the attenuating capacitor Cdamp must be lower than the ohmic attenuation resistance in the case of the undesired rise in the cut-off frequency (usually below 10 kHz), so that the attenuating capacitor can be effective.
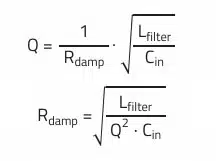
It is desirable that the quality factor Q of this undesirable resonant circuit is in the range of 0.5 to 0.8. A quality factor in this range ensures a resonant circuit that is neither over-attenuated nor under-attenuated and prevents the undesirable impedance rise at the cut off frequency, which could violate the stability criterion.
The equation above can be used to determine the required ohmic part Rdamp in the resonant circuit for a desired quality factor Q = 0.5…0.8. This can be the frequency dependent ESR of the attenuation capacitor, or an external resistor. The formula shows that the lowest possible filter inductance is advantageous, as the quality factor Q therefore does not become too high.
EMC Filter Designer
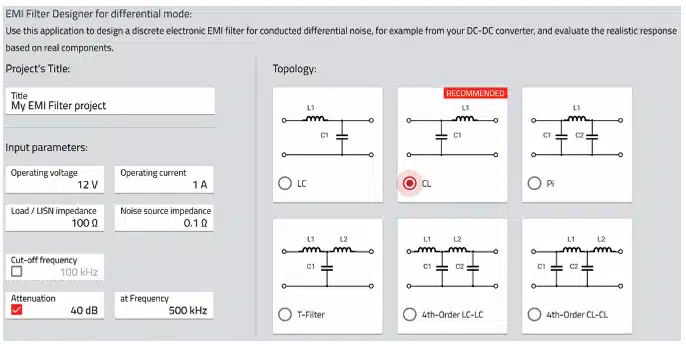
With the help of a new module, the “EMC Filter Designer” as part of the REDEXPERT tool, the developer can now select the required filter components quickly and easily.
The impedance of the interference source is determined from the input capacitor of the DC/DC converter, therefore a reference value of 0.1 Ω can be assumed here. As this is a pure differential mode filter design, 100 Ω should be entered for the LISN impedance. Based on these impedance conditions and the desired attenuation, the tool suggests a suitable filter topology. As an alternative to attenuation, a filter cut-off frequency (usually 1/10 of the switching frequency) can also be entered as a selection criterion.
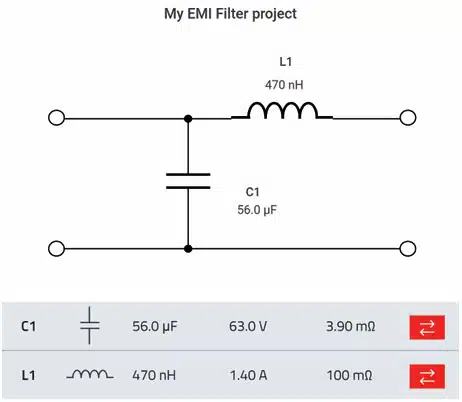
The components in Figure 6. are selected based on the current and voltage specifications from the first input page but can also be changed at any time. Manual selection of components is accomplished by selecting the double arrow symbol on the right. This brings up a list of suitable articles or the user may add specific parts. The resulting insertion loss, input and output impedance are plotted immediately. The summary tab compiles the BOM and plots into one
document as shown in Figure 7.
further reference link: EMC Filters Explained – from Component to Design; WE Webinar