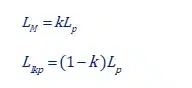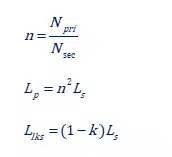Sotiris Zorbas, Power Εlectronics Εngineer of Frenetic in this blog explains how to build a transformer model in LTspice or Suzuka from measurements of a physical transformer.
The Transformer Model
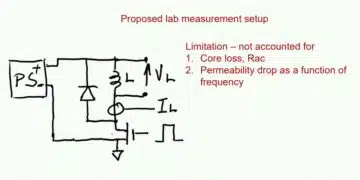
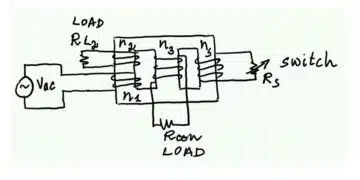
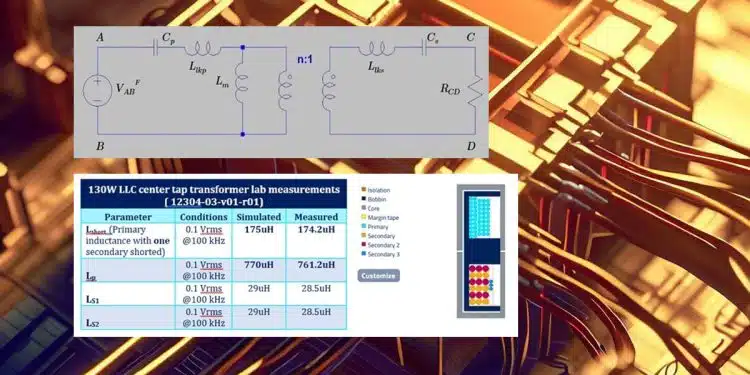
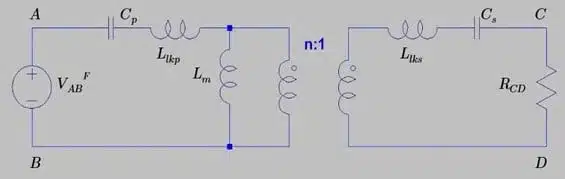
In Figure 1, if we omit the capacitors Cp, Cs we have a power source, a Transformer model, and a load resistor. Adding the series capacitor, we have the trending CLLC topology that is currently trending in the automotive world.
Can you believe I took this picture 7 years ago, when I was writing my thesis for the development of a complete wireless power system (WPT)? The industry back then hadn’t made the decision to move electric just yet (“thanks, Elon”). Back then, wireless power transfer was a trending topic with multiple new papers published across the globe. Mainly, the goal of the research groups was to explain the various modes of operation of WPT systems.
Figure 1 depicts the SS WPT topology because the capacitors are connected in series with Transformer. The only major difference between an SS WPT system and a CLLC Converter is the coupling factor k, not considering operation modes. You see in a WPT system, the inductors are facing each other and behave like a loosely coupled transformer.
Useful definitions and the connection to measurements
First of all:
- LP is the primary inductance.
- LM is the magnetizing inductance.
- Llkp is the primary leakage inductance.
When we build an inductor and choose x turns, given the AL value of the material, we get the inductance L=x2AL. If that is the primary winding of a Transformer, we call this inductance, primary inductance LP . Now, if the Transformer was an ideal one, then the coupling factor is equal to 1, and there are zero leakage inductances.
In the case of a real Transformer, as modelled in Figure 1, the primary “isn’t coupled” to the secondary completely, so LP is split between the leakage and the magnetizing inductance, depending on the coupling factor. The magnetizing inductance is the largest percentage of the primary inductance, responsible for power transfer, whilst the rest acts like an inductor storing energy in series.
Usually, the coupling factor k has values like 0.999, so almost all primary inductance is magnetizing inductance with a tiny percentage of it is left as leakage inductance Llkp. But in a WPT application, or in a resonant topology like LLC or CLLC, the coupling factor can take much lower values.
Also:
- Turns ratio n is known
- LP is known from the AL value and turns and can be easily measured if we just measure the primary inductance with all other windings open
- The coupling k factor is not known. If we know k, then we can calculate the primary and secondary leakage inductances and the Transformer model of Figure 1 is complete!
Do you know how to measure the k factor?
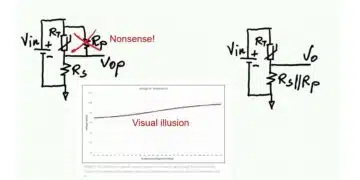
If your answer is “what do I need the k factor for, I just short the secondary and measure the leakage in the primary, which I call primary leakage”, then you’re right only if you assume the k factor is very close to unity.
When however, you design resonant Transformers you are about to commit mistakes thinking that way! Let’s look at what exactly happens if we short the secondary winding and measure from the primary side:
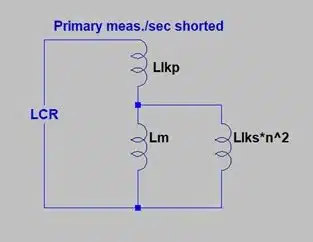
As seen in Figure 2, we don’t measure the primary leakage, but more correctly the “lumped”/ “effective”/ “total” leakage of the transformer that way. Well, that leakage is close to the primary leakage if we assume that the secondary leakage inductance is much lower than the magnetizing inductance, thus the parallel combo value is close to zero. You see the fault in these assumptions…
Instead of assumptions, we can write the following for the equation:
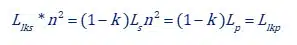
So, the total inductance which I like to call Lshort is:
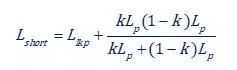
And after a page long of equation manipulations:
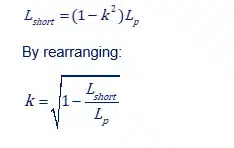
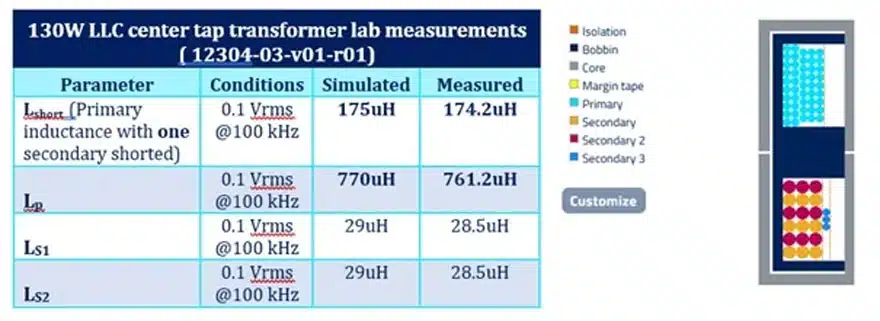
Now you can easily calculate k with this easy measurement and define all leakage inductances exactly. An example:
Calculating the k factor (in an LLC- center tap the short test is done with one of the 2 secondaries):
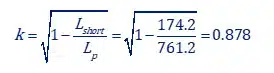
So:

One key skill is connecting theory and practice, with knowledge about parasitic elements and assumptions made in the process, no matter of the subject.